好的，以下是关于“为什么调和级数发散”的文章标题和内容：

标题：揭秘调和级数的发散之谜

内容：

当我们谈论调和级数时，我们指的是一个无穷数列，其每一项都是自然数的倒数。然而，这个看似简单的数列却隐藏着一个大秘密——它是一个发散数列。那么，为什么调和级数会发散呢？让我们一起来揭示这个神秘的现象。

首先，我们需要了解调和级数的定义和特性。调和级数的每一项都是形如 1/n 的形式，其中 n 是自然数。由于分母不断增大，数列的每一项会变得越来越小。但问题在于这是一个无穷数列，尽管相邻项之间的差距越来越小，但是每个项的数值并不会减少至零。因此，无论我们如何尝试计算这个数列的和，它都会无限增长下去。这就是调和级数的发散现象。

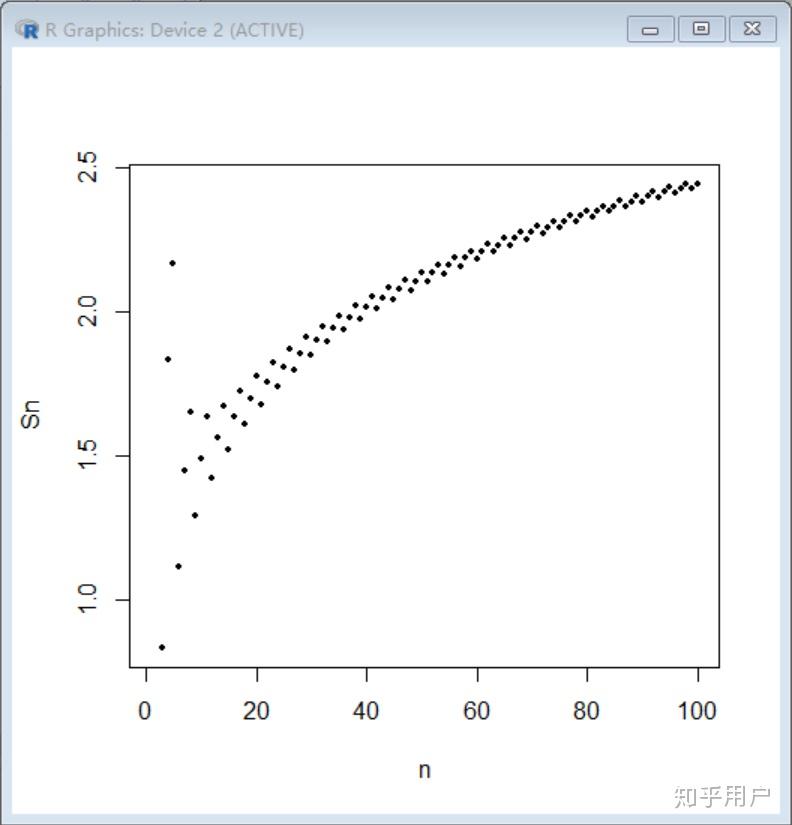
其次，我们可以从数学的角度分析调和级数的发散原因。调和级数的通项公式是 Hn = Σ(1/n)，其中 n 是自然数集合。这个数列的和会随着自然数的增加无限增大，因为每一项都是正数且不会消失。因此，即使每一项的值很小，由于无穷多的项相加，总和会无限增大，导致调和级数发散。这种现象在数学上被称为无穷大序列的发散性。

最后，我们可以从实际应用中进一步理解调和级数的发散性。尽管单个项的数值较小，但在许多实际问题中涉及到无穷多的项相加时，例如微积分中的积分问题或者概率统计中的期望值计算等，我们必须考虑到无穷大的总和可能会带来不可预测的结果。因此，理解调和级数的发散性对于解决这些问题至关重要。通过揭示调和级数发散的原因，我们可以更好地理解无穷大序列的性质和应用。希望这篇文章能够引起大家对调和级数的好奇和兴趣，让我们共同探索这个有趣而又神秘的现象吧！