【电机仿真】空间矢量脉宽调制(SVPWM)算法与实现
前言
���章【电机仿真】永磁同步电机模型中所提及了PMSM数学模型,模型+算法是电机控制的理论基础,但在实际控制中,需要将这两部分具象化。实际电机所需要的总是三相电流或者电压,控制对象为逆变器中的开关器件,我们需要将控制目标通过逆变器来实现,就需要建立起电流电压与逆变器开关元件之间的函数关系,该关系称之为空间矢量脉宽调制(SVPWM)算法。不管是理论还是试验,SVPWM算法总是绕不开的一点,在系统介绍矢量控制之前,需要掌握该算法的原理与实现,这有助于后续的电机控制开发。
一、空间矢量脉宽调制(SVPWM)算法
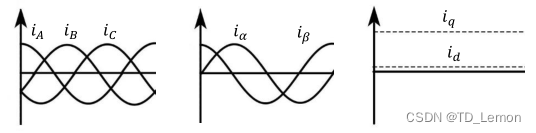
在之前的文章中介绍了三种坐标系下的PMSM模型,这三种坐标之间是通过Park和Clark变换得来,以电流为例如图1所示,通过上述两步变换,可将正弦变换的矢量等效为恒定常数,此时即可通过控制dq轴的电流实现PMSM控制。
图1 三相电流矢量等效输出电流分量PMSM实际输出转矩为:
T e = 1.5 n p [ φ f i q + ( L d − L q ) i d i q ] (1) {T_e} = 1.5{n_p}\left[ {{\varphi _f}{i_q} + \left( {{L_d} - {L_q}} \right){i_d}{i_q}} \right]\tag{1} Te=1.5np[φfiq+(Ld−Lq)idiq](1)
当满足 i d = 0 {i_d} = 0 id=0条件后,上式可变为:
T e = 1.5 n p φ f i q (2) {T_e} = 1.5{n_p}{\varphi _f}{i_q}\tag{2} Te=1.5npφfiq(2)
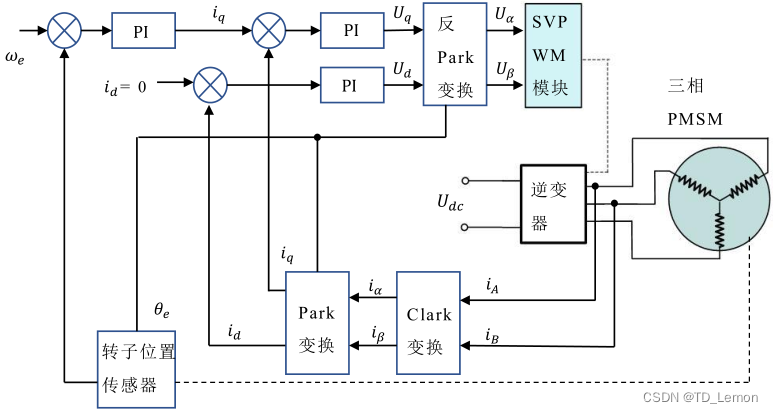
即可通过控制 i q {i_q} iq实现 T e {T_e} Te控制,以 i d = 0 {i_d} = 0 id=0矢量控制为例算法框图如下:
图2 i_d=0矢量控制算法由图2可得,将采集到的三相信号通过Park、Clark变换至DQ轴后,即可获得DQ轴参考电流,之后通过反Park变换与SVPWM算法,实时控制逆变器的3组IGBT就可以实现PMSM控制。在算法执行过程中,通过采样电机三相电流并将其通过Park、Clark变换至DQ轴上,通过 i d = 0 {i_d} = 0 id=0矢量控制给出相应的 i q {i_q} iq,但此时仍需要将其变为实际可控的三项信号。
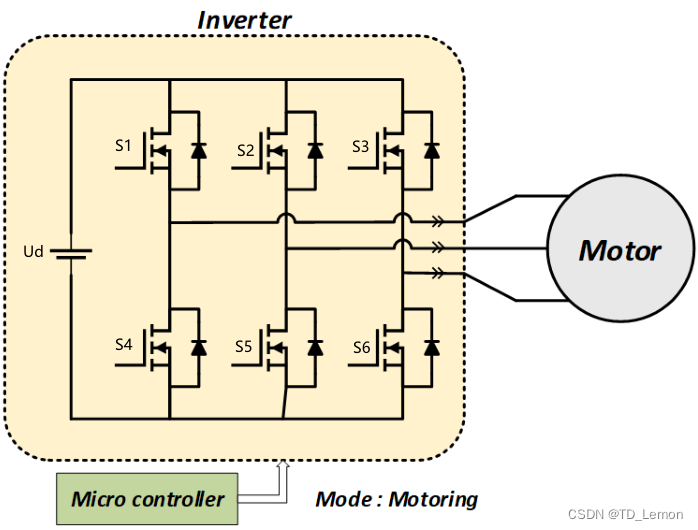
在实际控制中,通过三相全控逆变器实现,其中实际控制对象为逆变器中的晶闸管,通过晶闸管开断与电压的函数关系实现电机控制,该函数关系即为SVPWM技术。
图3 三相逆变桥电路如图2所示,共有三组六个IGBT开关,其中上桥和下桥开关互补,规定状态0为上桥开通下桥关断,规定状态1为下桥开通上桥关断,则三组开关对应八种开关状态:[000]、[001]、[010]、[011]、[100]、[101]、[110]、[111],则电机端线电压对应的开关函数为:
{ u A = 2 3 U d ( S 14 − 1 2 S 25 − 1 2 S 36 ) u B = 2 3 U d ( S 25 − 1 2 S 14 − 1 2 S 36 ) u C = 2 3 U d ( S 36 − 1 2 S 25 − 1 2 S 14 ) (3) \left\{ \begin{array}{l} {u_A} = \frac{2}{3}{U_d}\left( {{S_{14}} - \frac{1}{2}{S_{25}} - \frac{1}{2}{S_{36}}} \right)\\ {u_B} = \frac{2}{3}{U_d}\left( {{S_{25}} - \frac{1}{2}{S_{14}} - \frac{1}{2}{S_{36}}} \right)\\ {u_C} = \frac{2}{3}{U_d}\left( {{S_{36}} - \frac{1}{2}{S_{25}} - \frac{1}{2}{S_{14}}} \right) \end{array} \right.\tag{3} ⎩ ⎨ ⎧uA=32Ud(S14−21S25−21S36)uB=32Ud(S25−21S14−21S36)uC=32Ud(S36−21S25−21S14)(3)
同时该相电压合成的空间矢量可表示为:
U S = 2 3 U d ( S 14 e j 0 + S 25 e j 2 3 π + S 36 e − j 2 3 π ) (4) {U_S} = \frac{2}{3}{U_d}\left( {{S_{14}}{e^{j0}} + {S_{25}}{e^{j\frac{2}{3}\pi }} + {S_{36}}{e^{ - j\frac{2}{3}\pi }}} \right)\tag{4} US=32Ud(S14ej0+S25ej32π+S36e−j32π)(4)
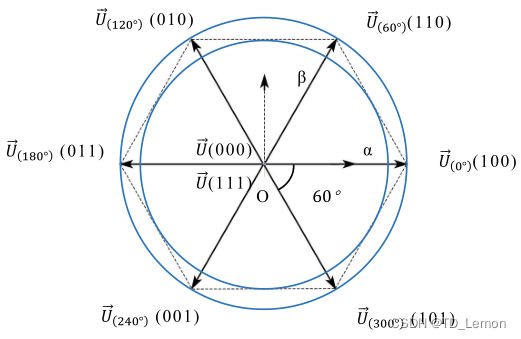
合成的电压矢量图如下:
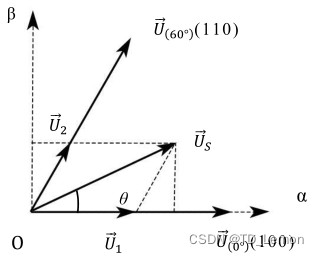
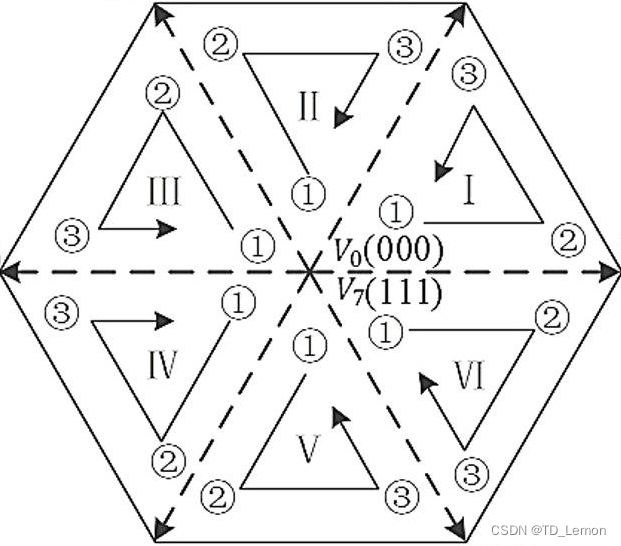
图4 电压空间矢量图由图4可知,通过开关组合将空间矢量划分为6个扇区,要想实现电机按照目标需求运行,就需要输入相应的目标电压矢量,结合式3、4可得,通过固定的开关组合可以得到电机需要的电压矢量,但是我们控制电压的方式为IGBT的通断时间,以第一扇区为例,
图5 第一扇区电压矢量图该扇区电压由[000]、[100]、[110]合成,开关开通时间依次记为 T 0 {T_0} T0、 T 1 {T_1} T1、 T 2 {T_2} T2,则开关时间 T S {T_S} TS可表示为:
T S = T 0 + T 1 + T 2 (5) {T_S} = {T_0} + {T_1} + {T_2}\tag{5} TS=T0+T1+T2(5)
为了合成所需的电压矢量,就需要计算出相应开关的开断时间。如图4,根据矢量分解的平衡原理可得:
T S ⋅ U S = T 0 ⋅ U ( 000 ) + T 1 ⋅ U ( 0 ∘ ) ( 100 ) + T 2 ⋅ U ( 60 ∘ ) ( 110 ) (6) {T_S} \cdot {U_S} = {T_0} \cdot U\left( {000} \right) + {T_1} \cdot {U_{\left( {{0^ \circ }} \right)}}\left( {100} \right) + {T_2} \cdot {U_{\left( {{{60}^ \circ }} \right)}}\left( {110} \right)\tag{6} TS⋅US=T0⋅U(000)+T1⋅U(0∘)(100)+T2⋅U(60∘)(110)(6)
则 U 1 {U_1} U1、 U 2 {U_2} U2可表示为:
{ U 1 = T 1 T S U ( 0 ∘ ) ( 100 ) U 2 = T 2 T S U ( 60 ∘ ) ( 110 ) (7) \left\{ \begin{array}{l} {U_1} = \frac{{{T_1}}}{{{T_S}}}{U_{\left( {{0^ \circ }} \right)}}\left( {100} \right)\\ {U_2} = \frac{{{T_2}}}{{{T_S}}}{U_{\left( {{{60}^ \circ }} \right)}}\left( {110} \right) \end{array} \right.\tag{7} {U1=TST1U(0∘)(100)U2=TST2U(60∘)(110)(7)
将 U 1 {U_1} U1、 U 2 {U_2} U2投影至 α 、 β \alpha、\beta α、β轴,可得:
{ U α = ∣ U 1 ∣ + ∣ U 2 ∣ cos 6 0 ∘ U β = ∣ U 2 ∣ sin 6 0 ∘ (8) \left\{ \begin{array}{l} {U_\alpha } = \left| {{U_1}} \right| + \left| {{U_2}} \right|\cos {60^ \circ }\\ {U_\beta } = \left| {{U_2}} \right|\sin {60^ \circ } \end{array} \right.\tag{8} {Uα=∣U1∣+∣U2∣cos60∘Uβ=∣U2∣sin60∘(8)
综上所述,当我们获得目标电压矢量之后,就能已知 U α 、 U β {U_\alpha }、 {U_\beta } Uα、Uβ进而可以计算出相应开关的开断时间,令 U ( 0 ∘ ) ( 100 ) 、 U ( 60 ∘ ) ( 110 ) {{U_{\left( {{0^\circ }} \right)}}\left( {100} \right)}、{{U_{\left( {{{60}^\circ }} \right)}}\left( {110} \right)} U(0∘)(100)、U(60∘)(110) 的模值为 U m = 2 3 U d {U_m} = \frac{2}{3}{U_d} Um=32Ud,联立式7、8可得:
{ T 0 = ( T S − T 1 − T 2 ) T 1 = ( U α − 1 3 U β ) ⋅ T S U m T 2 = 2 3 U β ⋅ T S U m (9) \left\{ \begin{array}{l} {T_0} = \left( {{T_S} - {T_1} - {T_2}} \right)\\ {T_1} = \left( {{U_\alpha } - \frac{1}{{\sqrt 3 }}{U_\beta }} \right) \cdot \frac{{{T_S}}}{{{U_m}}}\\ {T_2} = \frac{2}{{\sqrt 3 }}{U_\beta } \cdot \frac{{{T_S}}}{{{U_m}}} \end{array} \right.\tag{9} ⎩ ⎨ ⎧T0=(TS−T1−T2)T1=(Uα−3 1Uβ)⋅UmTST2=3 2Uβ⋅UmTS(9)
上式中 U α 、 U β {U_\alpha }、 {U_\beta } Uα、Uβ为 U S {U_S } US在 α β \alpha \beta αβ轴上的分量,
{ U α = ∣ U S ∣ ⋅ cos θ U β = ∣ U S ∣ ⋅ sin θ (10) \left\{ \begin{array}{l} {U_\alpha } = \left| {{U_S}} \right| \cdot \cos \theta \\ {U_\beta } = \left| {{U_S}} \right| \cdot \sin \theta \end{array} \right.\tag{10} {Uα=∣US∣⋅cosθUβ=∣US∣⋅sinθ(10)
将式10代入式9中可得:
{ T 0 = T S − T 1 − T 2 T 1 = 3 ∣ U S ∣ U d T S ⋅ sin ( π 3 − θ ) T 2 = 3 ∣ U S ∣ U d T S ⋅ sin θ (11) \left\{ \begin{array}{l} {T_0} = {T_S} - {T_1} - {T_2}\\ {T_1} = \sqrt 3 \frac{{\left| {{U_S}} \right|}}{{{U_d}}}{T_S} \cdot \sin \left( {\frac{\pi }{3} - \theta } \right)\\ {T_2} = \sqrt 3 \frac{{\left| {{U_S}} \right|}}{{{U_d}}}{T_S} \cdot \sin \theta \end{array} \right.\tag{11} ⎩ ⎨ ⎧T0=TS−T1−T2T1=3 Ud∣US∣TS⋅sin(3π−θ)T2=3 Ud∣US∣TS⋅sinθ(11)
上式中 U S {U_S} US为驱动电机所需要的电压矢量, U d {U_d} Ud为逆变器输入直流电压大小。
二、SVPWM技术的实现
上一小节以合成第一扇区电压矢量为例,简单介绍了SVPWM合成的原理,但是实际所需要合成的电压矢量可能出现在任意扇区,故实际SVPWM技术的实现与第二小节的理论存在差距。SVPWM的实现通常分为两步:
- 判断扇区
- 计算作用时间
2.1判断扇区
由图2可得在SVPWM算法之前,需要将 U d U q {U_d}{U_q} UdUq通过反Park变换,转换至 α β \alpha \beta αβ轴上,并开展SVPWM。这次定义中间变量X、Y、Z,
{ X = U β Y = 3 2 U α − 1 2 U β Z = − 3 2 U α − 1 2 U β (12) \left\{ \begin{array}{l} X = {U_\beta }\\ Y = \frac{{\sqrt 3 }}{2}{U_\alpha } - \frac{1}{2}{U_\beta }\\ Z = - \frac{{\sqrt 3 }}{2}{U_\alpha } - \frac{1}{2}{U_\beta } \end{array} \right.\tag{12} ⎩ ⎨ ⎧X=UβY=23 Uα−21UβZ=−23 Uα−21Uβ(12)
根据X、Y、Z的正负依次给定x、y、z的值,前者为正,后者取1,前者非正,后者取0,令 N = x + 2 y + 4 z N = x + 2y + 4z N=x+2y+4z,即可通过N的取值来判断电压矢量扇区,如下表所示:
表1 电压矢量扇区判断| N | 3 | 1 | 5 | 4 | 6 | 2 |
|---|---|---|---|---|---|---|
| 扇区 | Ⅰ | Ⅱ | Ⅲ | Ⅳ | Ⅴ | Ⅵ |
2.2计算作用时间
联立式7、8可得:
{ U α = T 1 T S ⋅ ∣ U ( 0 ∘ ) ( 100 ) ∣ + T 2 T S ∣ U ( 60 ∘ ) ( 110 ) ∣ ⋅ cos 6 0 ∘ U β = T 2 T S ∣ U ( 60 ∘ ) ( 110 ) ∣ ⋅ sin 6 0 ∘ (13) \left\{ \begin{array}{l} {U_\alpha } = \frac{{{T_1}}}{{{T_S}}} \cdot \left| {{U_{\left( {{0^\circ }} \right)}}\left( {100} \right)} \right| + \frac{{{T_2}}}{{{T_S}}}\left| {{U_{\left( {{{60}^\circ }} \right)}}\left( {110} \right)} \right| \cdot \cos {60^ \circ }\\ {U_\beta } = \frac{{{T_2}}}{{{T_S}}}\left| {{U_{\left( {{{60}^\circ }} \right)}}\left( {110} \right)} \right| \cdot \sin {60^ \circ } \end{array} \right.\tag{13} {Uα=TST1⋅ U(0∘)(100) +TST2 U(60∘)(110) ⋅cos60∘Uβ=TST2 U(60∘)(110) ⋅sin60∘(13)
化简式13可得矢量作用时间:
{ T 1 = ( U α − 1 3 U β ) ⋅ T S U m T 2 = 2 3 U β ⋅ T S U m (14) \left\{ \begin{array}{l} {T_1} = \left( {{U_\alpha } - \frac{1}{{\sqrt 3 }}{U_\beta }} \right) \cdot \frac{{{T_S}}}{{{U_m}}}\\ {T_2} = \frac{2}{{\sqrt 3 }}{U_\beta } \cdot \frac{{{T_S}}}{{{U_m}}} \end{array} \right.\tag{14} {T1=(Uα−3 1Uβ)⋅UmTST2=3 2Uβ⋅UmTS(14)
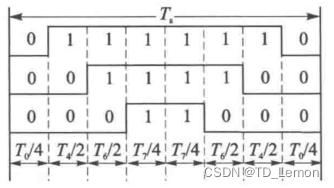
上述计算的矢量作用时间 T 1 、 T 2 {T_1}、{T_2} T1、T2为Ⅰ区两个矢量的总作用时间,为了合成该区的电压矢量需要来回切换开关组合,不同开关组合对应着不同的逆变器状态,为了最小化开关变换,算法需要保证每次切换仅改变一组开关,最终形成了七段式或五段式SVPWM,以七段式合成Ⅰ区电压矢量为例,如下图所示:
图6 七段式Ⅰ区开关顺序为了将Ⅰ区规律应用至所有区域,定义中间变量A、B、C,
{ A = 2 T S 3 U S ⋅ U β B = 2 T S 3 U S ⋅ ( 3 2 U α + 1 2 U β ) C = 2 T S 3 U S ⋅ ( − 3 2 U α + 1 2 U β ) (13) \left\{ \begin{array}{l} A = \frac{{2{T_S}}}{{\sqrt 3 {U_S}}} \cdot {U_\beta }\\ B = \frac{{2{T_S}}}{{\sqrt 3 {U_S}}} \cdot \left( {\frac{{\sqrt 3 }}{2}{U_\alpha } + \frac{1}{2}{U_\beta }} \right)\\ C = \frac{{2{T_S}}}{{\sqrt 3 {U_S}}} \cdot \left( { - \frac{{\sqrt 3 }}{2}{U_\alpha } + \frac{1}{2}{U_\beta }} \right) \end{array} \right.\tag{13} ⎩ ⎨ ⎧A=3 US2TS⋅UβB=3 US2TS⋅(23 Uα+21Uβ)C=3 US2TS⋅(−23 Uα+21Uβ)(13)
由上式可得,电压矢量作用时间如下表所示:
表2 电压矢量作用时间| N | 3 | 1 | 5 | 4 | 6 | 2 |
|---|---|---|---|---|---|---|
| T f i r s t {T_{first}} Tfirst | -C | C | A | -A | -B | B |
| T s e c o n d {T_{second}} Tsecond | A | B | -B | C | -C | -A |
| T 0 \ T 7 {T_0}\backslash {T_7} T0\T7 | 1 2 ( T s − T 1 − T 2 ) \dfrac{1}{2}\left( T_{s}-T_{1}-T_{2}\right) 21(Ts−T1−T2) |
上表中 T f i r s t 、 T s e c o n d {T_{first}}、{T_{second}} Tfirst、Tsecond分别为每个扇区中的最顺时针基本向量、最逆时针基本向量,所有扇区的顺时针方向如下图所示:
图7 6扇区基本矢量切换方向倘若 T f i r s t + T s e c o n d > T s {T_{first}} + {T_{second}}>{T_s} Tfirst+Tsecond>Ts,则对其过调制处理:
{ T f i r s t = T f i r s t T f i r s t + T s e c o n d T s T s e c o n d = T s e c o n d T f i r s t + T s e c o n d T s (14) \left\{ \begin{array}{l} {T_{first}} = \frac{{{T_{first}}}}{{{T_{first}} + {T_{second}}}}{T_s}\\ {T_{second}} = \frac{{{T_{second}}}}{{{T_{first}} + {T_{second}}}}{T_s} \end{array} \right.\tag{14} {Tfirst=Tfirst+TsecondTfirstTsTsecond=Tfirst+TsecondTsecondTs(14)
2.3确定切换时间点
以图6为例,一个周期内需要包括两个非零向量和两个零向量共同作用,由图6结合表2,定义时间变量 T a 、 T b 、 T c {T_a}、{T_b}、{T_c} Ta、Tb、Tc,表示如下:
{ T a = T 0 2 = T 7 2 = T S − T f i r s t − T s e c o n d 4 T b = T a + T f i r s t 2 T c = T b + T s e c o n d 2 (15) \left\{ \begin{array}{l} {T_a} = \frac{{{T_0}}}{2} = \frac{{{T_7}}}{2} = \frac{{{T_S} - {T_{first}} - {T_{second}}}}{4}\\ {T_b} = {T_a} + \frac{{{T_{first}}}}{2}\\ {T_c} = {T_b} + \frac{{{T_{second}}}}{2} \end{array} \right.\tag{15} ⎩ ⎨ ⎧Ta=2T0=2T7=4TS−Tfirst−TsecondTb=Ta+2TfirstTc=Tb+2Tsecond(15)
则所有扇区的切换时间点总结为下表:
表3 扇区切换时间点| N | 3 | 1 | 5 | 4 | 6 | 2 |
|---|---|---|---|---|---|---|
| T c m 1 {T_{cm1}} Tcm1 | T a {T_a} Ta | T b {T_b} Tb | T c {T_c} Tc | T c {T_c} Tc | T b {T_b} Tb | T a {T_a} Ta |
| T c m 2 {T_{cm2}} Tcm2 | T b {T_b} Tb | T a {T_a} Ta | T a {T_a} Ta | T b {T_b} Tb | T c {T_c} Tc | T c {T_c} Tc |
| T c m 3 {T_{cm3}} Tcm3 | T c {T_c} Tc | T c {T_c} Tc | T b {T_b} Tb | T a {T_a} Ta | T a {T_a} Ta | T b {T_b} Tb |
三、总结
本文以Ⅰ扇区为例介绍了SVPWM算法原理与实现过程,其中实现过程共包含三步:判断扇区、计算作用时间、确定切换时间点。后续将补充matlab的仿真文件供大家参考。