CCF CSP 202006-4 1246 （100分详细题解，矩阵乘法+快速幂）

202006-4 1246 （100分详细题解，矩阵乘法+快速幂）

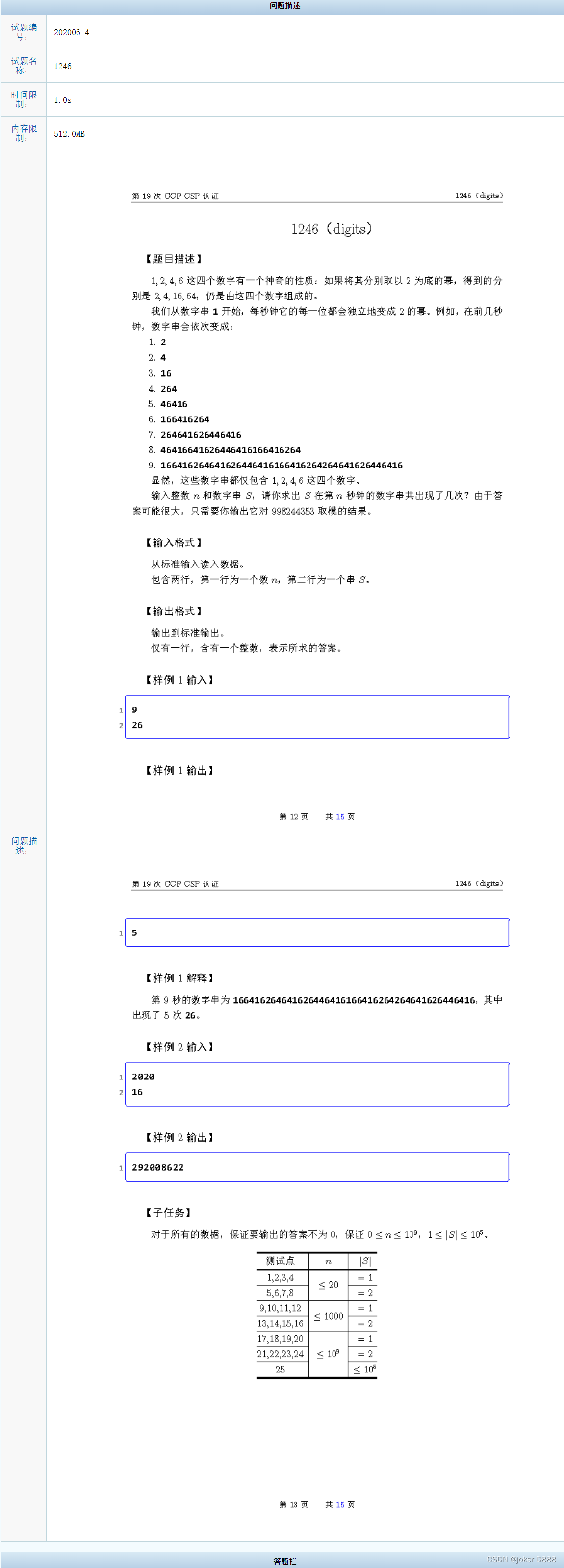
可以先���下csp官方的思路讲解，大思路是状态转移，先看下面s 2 2 -> 4 4 -> 16 6 -> 6 64 4 16 -> 26（不考虑2，6，4，64的原因是，16可以拆分为1和6，而1->2 , 6-> 64, 6, 4，去除冗余解) ... 详细见尾部代码

s2时，可以进行倒推，如：464 上一次由 26操作而来。同时考虑到题目给的s是一个部分数字串，故可能无法直接倒推回s=2，故s在整个序列的情况，可能分为s前面是1，s前面是6，或者s前面不是1或6， 因为4->16 6->64,都会产生两位，所以s的首个数字可能是16中的6，以及64中的6，由于s只是其中的一部分，所以我们要在前面补上1和6。你可能回想为什么不在后面补1和6，其实也考虑了，不过在代码中用i + 1 == str.size()来解决了。

#include 
using namespace std;
typedef long long LL;
const int N = 14, MOD = 998244353;
int n;
string S;
int id[100];        // id[x]将x映射到0~13
vector vers{
    1, 2, 4, 6, 16, 26, 41, 42, 44,
    46, 61, 62, 64, 66
};
// 上面的数字进行运算后可以得出下面的贡献，两位数字的运算后的数字只有一个
// 如16->26（不考虑2，6，4，64的原因是，16可以拆分为1和6，而1->2 , 6->64, 6, 4)
// 故两位数字运算后只转移到前一位数字幂的后一位和后一位数字幂的前一位
// 当s的长度大于2时，我们可以根据转移的规律，逆推到s只有两位的情况。
// s在整个序列的情况，可能分为s前面是1，s前面是6，或者s前面不是1或6.
// 因为4->16 6->64,都会产生两位，所以s的首个数字可能是16中的6，以及64中的6，由于s只是其中的一部分，所以我们要补上1和6
vector g{
    {2}, {4}, {1, 6, 16}, {6, 4, 64}, {26},
    {46}, {62}, {64}, {61}, {66}, {42},
    {44}, {41}, {46}
};
int tr[N][N];       // tr的第j列是对ver[j]的贡献
void init() {
    memset(id, -1, sizeof id);
    for (int i = 0; i >= 1;
    }
    return res[0][id];
}
string get(string str) {
    string res;
    for (int i = 0; i  n >> S;
    cout