python coding with ChatGPT жү“еҚЎз¬¬22еӨ©| дәҢеҸүжҗңзҙўж ‘зҡ„ж“ҚдҪңпјҡжҸ’е…ҘгҖҒеҲ йҷӨгҖҒдҝ®еүӘгҖҒиҪ¬жҚў
зӣёе…іжҺЁиҚҗ
python coding with ChatGPT жү“еҚЎз¬¬12еӨ©| дәҢеҸүж ‘пјҡзҗҶи®әеҹәзЎҖ
python coding with ChatGPT жү“еҚЎз¬¬13еӨ©| дәҢеҸүж ‘зҡ„ж·ұеәҰдјҳе…ҲйҒҚеҺҶ
python coding with ChatGPT жү“еҚЎз¬¬14еӨ©| дәҢеҸүж ‘зҡ„е№ҝеәҰдјҳе…ҲйҒҚеҺҶ
python coding with ChatGPT жү“еҚЎз¬¬15еӨ©| дәҢеҸүж ‘пјҡзҝ»иҪ¬дәҢеҸүж ‘гҖҒеҜ№з§°дәҢеҸүж ‘
python coding with ChatGPT жү“еҚЎз¬¬16еӨ©| дәҢеҸүж ‘пјҡе®Ңе…ЁдәҢеҸүж ‘гҖҒе№іиЎЎдәҢеҸүж ‘гҖҒдәҢеҸүж ‘зҡ„жүҖжңүи·Ҝеҫ„гҖҒе·ҰеҸ¶еӯҗд№Ӣе’Ң
python coding with ChatGPT жү“еҚЎз¬¬17еӨ©| дәҢеҸүж ‘пјҡжүҫж ‘е·ҰдёӢи§’зҡ„еҖјгҖҒи·Ҝеҫ„жҖ»е’Ң
python coding with ChatGPT жү“еҚЎз¬¬18еӨ©| дәҢеҸүж ‘пјҡд»ҺдёӯеәҸдёҺеҗҺеәҸйҒҚеҺҶеәҸеҲ—жһ„йҖ дәҢеҸүж ‘гҖҒжңҖеӨ§дәҢеҸүж ‘
python coding with ChatGPT жү“еҚЎз¬¬19еӨ©| дәҢеҸүж ‘пјҡеҗҲ并дәҢеҸүж ‘
python coding with ChatGPT жү“еҚЎз¬¬20еӨ©| дәҢеҸүжҗңзҙўж ‘пјҡжҗңзҙўгҖҒйӘҢиҜҒгҖҒжңҖе°Ҹз»қеҜ№е·®гҖҒдј—ж•°
python coding with ChatGPT жү“еҚЎз¬¬21еӨ©| дәҢеҸүж ‘пјҡжңҖиҝ‘е…¬е…ұзҘ–е…Ҳ
ж–Үз« зӣ®еҪ•
- дәҢеҸүжҗңзҙўж ‘зҡ„жҸ’е…Ҙж“ҚдҪң
- Key Points
- зӣёе…ійўҳзӣ®
- и§Ҷйў‘и®Іи§Ј
- йҮҚзӮ№еҲҶжһҗ
- еҲ йҷӨдәҢеҸүжҗңзҙўж ‘зҡ„иҠӮзӮ№
- Key Points
- зӣёе…ійўҳзӣ®
- и§Ҷйў‘и®Іи§Ј
- йҮҚзӮ№еҲҶжһҗ
- дҝ®еүӘдәҢеҸүжҗңзҙўж ‘
- Key Points
- зӣёе…ійўҳзӣ®
- и§Ҷйў‘и®Іи§Ј
- йҮҚзӮ№еҲҶжһҗ
- е°ҶжңүеәҸж•°з»„иҪ¬жҚўдёәдәҢеҸүжҗңзҙўж ‘
- Key Points
- зӣёе…ійўҳзӣ®
- и§Ҷйў‘и®Іи§Ј
- йҮҚзӮ№еҲҶжһҗ
- жҠҠдәҢеҸүжҗңзҙўж ‘иҪ¬жҚўдёәзҙҜеҠ ж ‘
- Key Points
- зӣёе…ійўҳзӣ®
- и§Ҷйў‘и®Іи§Ј
- йҮҚзӮ№еҲҶжһҗ
дәҢеҸүжҗңзҙўж ‘зҡ„жҸ’е…Ҙж“ҚдҪң
Key Points
BSTзҡ„жҖ§иҙЁпјҡеҜ№дәҺжҜҸдёӘиҠӮзӮ№пјҢе…¶е·Ұеӯҗж ‘еҸӘеҢ…еҗ«е°ҸдәҺеҪ“еүҚиҠӮзӮ№зҡ„ж•°пјҢе…¶еҸіеӯҗж ‘еҸӘеҢ…еҗ«еӨ§дәҺеҪ“еүҚиҠӮзӮ№зҡ„ж•°гҖӮ
зӣёе…ійўҳзӣ®
701. дәҢеҸүжҗңзҙўж ‘зҡ„жҸ’е…Ҙж“ҚдҪң
и§Ҷйў‘и®Іи§Ј
дәҢеҸүжҗңзҙўж ‘зҡ„жҸ’е…Ҙж“ҚдҪң
йҮҚзӮ№еҲҶжһҗ
ж–№жі•дёҖпјҡйҖ’еҪ’жі•
def insertIntoBST(root, val): # еҰӮжһңеҪ“еүҚиҠӮзӮ№дёәз©әпјҢеҲӣе»әдёҖдёӘж–°иҠӮзӮ№е№¶иҝ”еӣһ if not root: return TreeNode(val) # еҰӮжһңж–°еҖје°ҸдәҺеҪ“еүҚиҠӮзӮ№зҡ„еҖјпјҢйҖ’еҪ’ең°жҸ’е…ҘеҲ°е·Ұеӯҗж ‘ if valж–№жі•дәҢпјҡиҝӯд»Јжі•
def insertIntoBST(root, val): if not root: return TreeNode(val) current = root while True: if val current.val if current.right: current = current.right else: current.right = TreeNode(val) break # жҸ’е…Ҙе®ҢжҲҗпјҢйҖҖеҮәеҫӘзҺҜ return rootеҲ йҷӨдәҢеҸүжҗңзҙўж ‘зҡ„иҠӮзӮ№
Key Points
еҲҶзұ»и®Ёи®әпјҡ
- жІЎжүҫеҲ°иҠӮзӮ№
- еҸ¶еӯҗиҠӮзӮ№
- еҸӘжңүдёҖдёӘеӯ©еӯҗзҡ„иҠӮзӮ№
- жңүдёӨдёӘеӯ©еӯҗзҡ„иҠӮзӮ№
зӣёе…ійўҳзӣ®
450. еҲ йҷӨдәҢеҸүжҗңзҙўж ‘з§Қзҡ„иҠӮзӮ№
и§Ҷйў‘и®Іи§Ј
и°ғж•ҙдәҢеҸүж ‘зҡ„з»“жһ„жңҖйҡҫ
йҮҚзӮ№еҲҶжһҗ
жҲ‘们йңҖиҰҒд»Һж №иҠӮзӮ№ејҖе§ӢпјҢдҪҝз”ЁдәҢеҸүжҗңзҙўж ‘зҡ„жҖ§иҙЁжқҘе®ҡдҪҚиҰҒеҲ йҷӨзҡ„иҠӮзӮ№гҖӮиҝҷж„Ҹе‘ізқҖпјҡ
еҰӮжһң key е°ҸдәҺеҪ“еүҚиҠӮзӮ№зҡ„еҖјпјҢеҲҷжҲ‘们еә”иҜҘеңЁе·Ұеӯҗж ‘дёӯжҹҘжүҫ keyгҖӮ
еҰӮжһң key еӨ§дәҺеҪ“еүҚиҠӮзӮ№зҡ„еҖјпјҢеҲҷжҲ‘们еә”иҜҘеңЁеҸіеӯҗж ‘дёӯжҹҘжүҫ keyгҖӮ
еҰӮжһң key зӯүдәҺеҪ“еүҚиҠӮзӮ№зҡ„еҖјпјҢйӮЈд№ҲжҲ‘们е°ұжүҫеҲ°дәҶиҰҒеҲ йҷӨзҡ„иҠӮзӮ№гҖӮ
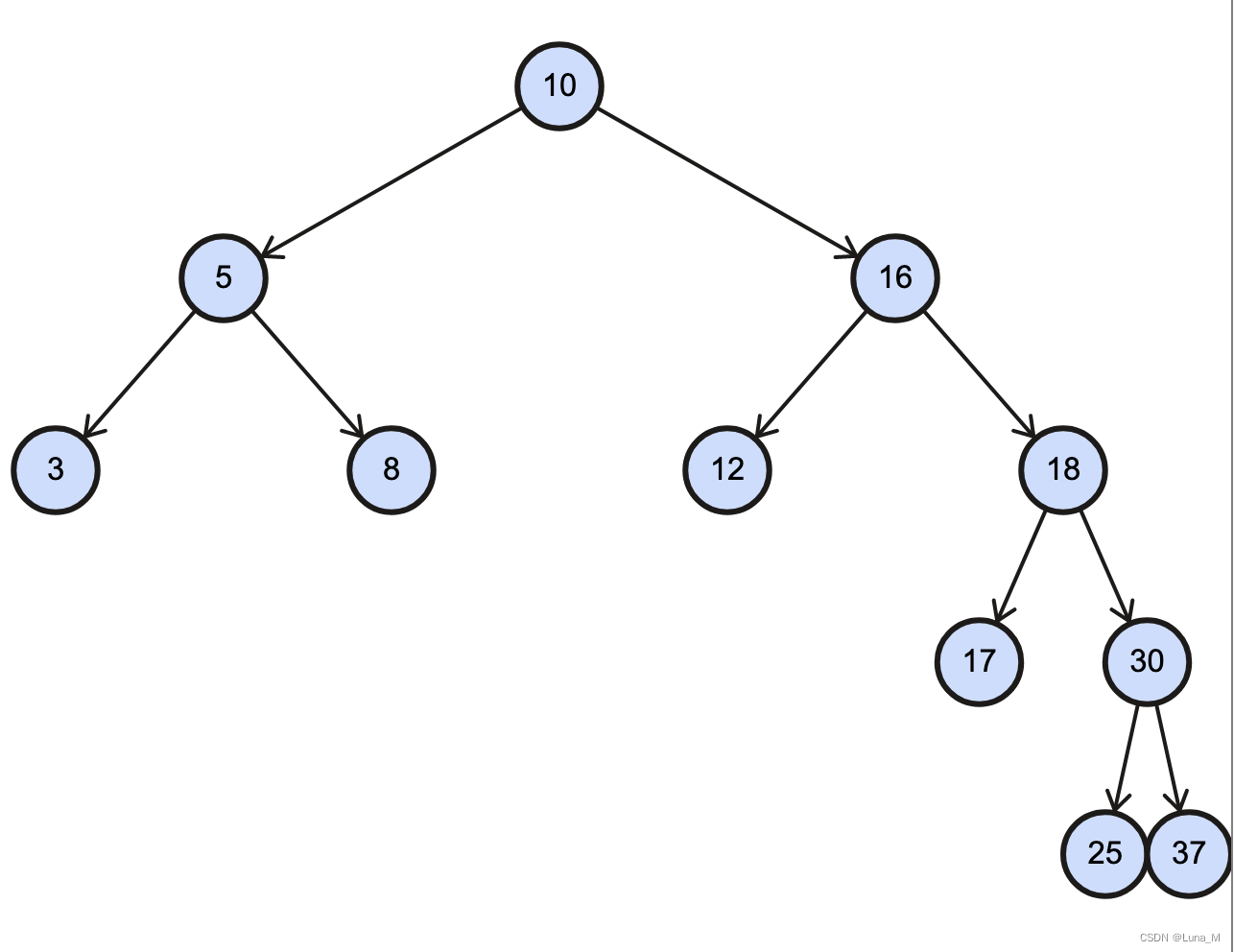
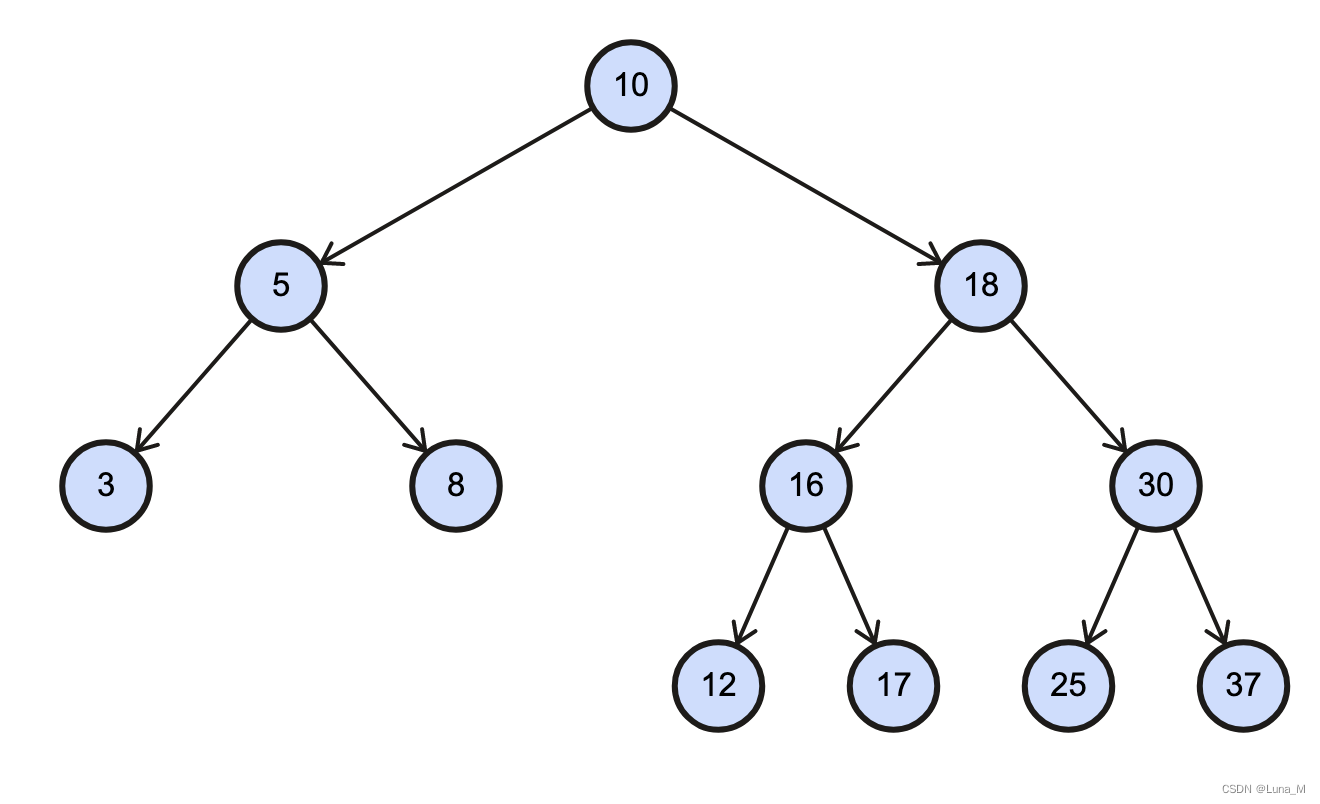
дҫӢеҰӮпјҡеҲ йҷӨеҰӮдёӢдәҢеҸүж ‘еҖјдёә20зҡ„иҠӮзӮ№
е…¶дёӯпјҢеҲ йҷӨжңүдёӨдёӘеӯ©еӯҗзҡ„иҠӮзӮ№жҳҜжңҖйҮҚиҰҒзҡ„пјҢдё»иҰҒжңүдёӨз§ҚжҖқи·Ҝпјҡ
- з”ЁеҲ йҷӨиҠӮзӮ№зҡ„е·Ұеӯ©еӯҗжӣҝжҚўеҲ йҷӨиҠӮзӮ№пјҢжҠҠеҲ йҷӨиҠӮзӮ№зҡ„еҸіеӯ©еӯҗж•ҙдёӘж”ҫеңЁе·Ұеӯ©еӯҗзҡ„жңҖеӨ§иҠӮзӮ№зҡ„еҸідҫ§гҖӮ
- дјҳзӮ№пјҡдёҚз”ЁйҖ’еҪ’и°ғз”ЁеҲ йҷӨиҠӮзӮ№зҡ„еҮҪж•°
- зјәзӮ№пјҡж–°дәҢеҸүж ‘з»“жһ„ж”№еҸҳдјҡеҫҲеӨ§пјҲеҰӮпјҡе№іиЎЎ->дёҚе№іиЎЎпјү
- з”ЁеҲ йҷӨиҠӮзӮ№зҡ„е·Ұеӯ©еӯҗзҡ„жңҖеӨ§еҖјжӣҝжҚўеҲ йҷӨиҠӮзӮ№пјҢ然еҗҺйҖ’еҪ’еҲ йҷӨе·Ұеӯ©еӯҗзҡ„жңҖеӨ§иҠӮзӮ№гҖӮ
- дјҳзӮ№пјҡж–°дәҢеҸүж ‘з»“жһ„еҸҳеҢ–иҫғе°Ҹ
- зјәзӮ№пјҡйңҖиҰҒйҖ’еҪ’и°ғз”Ё
ж–№жі•дёҖпјҡ
ж–№жі•дёҖпјҡ
йҖ’еҪ’жі•пјҡ
def get_max_child(node): while node.right: node = node.right return node def deleteNode(root, key): if not root: return root if root.val > key: root.left = deleteNode(root.left, key) return root # иҝ”еӣһrootжүҚе®Ңж•ҙ if root.valеҶҷйҖ’еҪ’зҡ„йҖ»иҫ‘пјҡ
жҹҗдёӘжғ…еҪўзҡ„йҖ»иҫ‘иҰҒе®Ңж•ҙпјҲreturnпјү
ж–№жі•дёҖпјҡ
иҝӯд»Јжі•
def deleteNode(root, key): current = root parent = None while current: if current.val > key: parent = current current = current.left elif current.valиҝӯд»Јжі•жіЁж„ҸиҖғиҷ‘parentдёәNoneзҡ„жғ…еҶө
ж–№жі•дәҢпјҡ
йҖ’еҪ’жі•
def deleteNode(root, key): if not root: return root if root.val > key: root.left = deleteNode(root.left, key) return root if root.valж–№жі•дәҢпјҡ
иҝӯд»Јжі•
current = root parent = None while current: if current.val > key: parent = current current = current.left elif current.valдҝ®еүӘдәҢеҸүжҗңзҙўж ‘
Key Points
жҳ“й”ҷзӮ№пјҡ
3 / \ 0 4 \ 2 / 1[1,3]
зӣёе…ійўҳзӣ®
669. дҝ®еүӘдәҢеҸүжҗңзҙўж ‘
и§Ҷйў‘и®Іи§Ј
еҰӮдҪ•дҝ®еүӘдәҢеҸүж ‘
йҮҚзӮ№еҲҶжһҗ
ж–№жі•дёҖпјҡ йҖ’еҪ’жі•
def trimBST(root, low, high): if not root: return None # еҰӮжһңиҠӮзӮ№еҖје°ҸдәҺlowпјҢйӮЈд№Ҳе®ғзҡ„е·Ұеӯҗж ‘йғҪдёҚеңЁиҢғеӣҙеҶ…пјҢеә”дҝ®еүӘжҺүе·Ұеӯҗж ‘ if root.val high: root = trimBST(root.left, low, high) # еҰӮжһңиҠӮзӮ№еҖјеңЁ[low, high]иҢғеӣҙеҶ…пјҢйҖ’еҪ’дҝ®еүӘе…¶е·ҰеҸіеӯҗж ‘ else: root.left = trimBST(root.left, low, high) root.right = trimBST(root.right, low, high) return rootж–№жі•дәҢпјҡиҝӯд»Јжі•
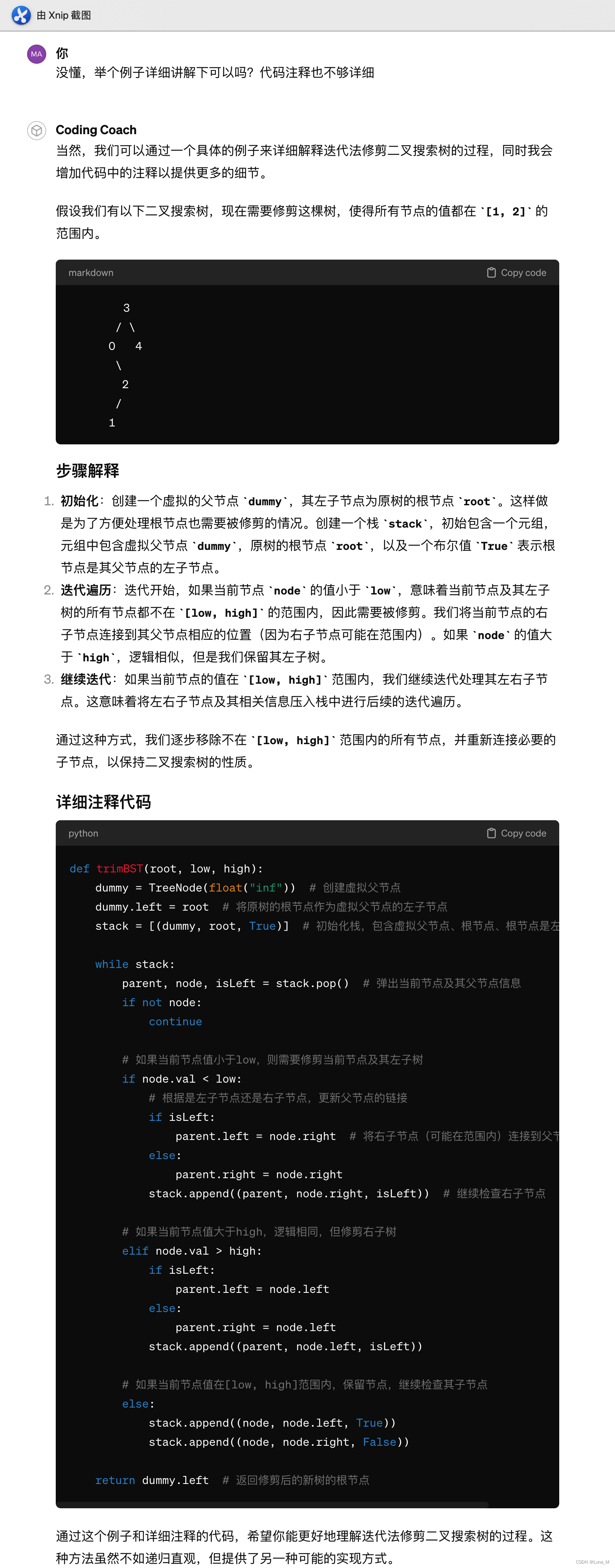
def trimBST(root, low, high): dummy = TreeNode(float("inf")) # еҲӣе»әиҷҡжӢҹзҲ¶иҠӮзӮ№ dummy.left = root # е°ҶеҺҹж ‘зҡ„ж №иҠӮзӮ№дҪңдёәиҷҡжӢҹзҲ¶иҠӮзӮ№зҡ„е·ҰеӯҗиҠӮзӮ№ stack = [(dummy, root, True)] # еҲқе§ӢеҢ–ж ҲпјҢеҢ…еҗ«иҷҡжӢҹзҲ¶иҠӮзӮ№гҖҒж №иҠӮзӮ№гҖҒж №иҠӮзӮ№жҳҜе·ҰеӯҗиҠӮзӮ№зҡ„дҝЎжҒҜ while stack: parent, node, isLeft = stack.pop() # еј№еҮәеҪ“еүҚиҠӮзӮ№еҸҠе…¶зҲ¶иҠӮзӮ№дҝЎжҒҜ if not node: continue # еҰӮжһңеҪ“еүҚиҠӮзӮ№еҖје°ҸдәҺlowпјҢеҲҷйңҖиҰҒдҝ®еүӘеҪ“еүҚиҠӮзӮ№еҸҠе…¶е·Ұеӯҗж ‘ if node.val high: if isLeft: parent.left = node.left else: parent.right = node.left stack.append((parent, node.left, isLeft)) # еҰӮжһңеҪ“еүҚиҠӮзӮ№еҖјеңЁ[low, high]иҢғеӣҙеҶ…пјҢдҝқз•ҷиҠӮзӮ№пјҢ继з»ӯжЈҖжҹҘе…¶еӯҗиҠӮзӮ№ else: stack.append((node, node.left, True)) stack.append((node, node.right, False)) return dummy.left # иҝ”еӣһдҝ®еүӘеҗҺзҡ„ж–°ж ‘зҡ„ж №иҠӮзӮ№иҝҷж®өд»Јз ҒдҪҝз”ЁдәҶдёҖдёӘж ҲжқҘиҝҪиёӘйҒҚеҺҶиҝҮзЁӢдёӯзҡ„иҠӮзӮ№д»ҘеҸҠе®ғ们зҡ„зҲ¶иҠӮзӮ№е’ҢжҳҜеҗҰдёәе·ҰеӯҗиҠӮзӮ№зҡ„дҝЎжҒҜгҖӮеҜ№жҜҸдёӘиҠӮзӮ№пјҢжҲ‘们жЈҖжҹҘе®ғжҳҜеҗҰйңҖиҰҒиў«дҝ®еүӘпјҲеҚіе®ғзҡ„еҖјжҳҜеҗҰеңЁ [low, high] иҢғеӣҙд№ӢеӨ–пјүгҖӮеҰӮжһңжҳҜпјҢеҲҷж №жҚ®е®ғжҳҜе·ҰеӯҗиҠӮзӮ№иҝҳжҳҜеҸіеӯҗиҠӮзӮ№пјҢжӣҙж–°зҲ¶иҠӮзӮ№зҡ„зӣёеә”й“ҫжҺҘгҖӮеҰӮжһңиҠӮзӮ№зҡ„еҖјеңЁиҢғеӣҙеҶ…пјҢжҲ‘们е°Ҷ继з»ӯеӨ„зҗҶе®ғзҡ„еӯҗиҠӮзӮ№гҖӮ
иҜ·жіЁж„ҸпјҢиҝҷдёӘж–№жі•иҷҪ然йҒҝе…ҚдәҶйҖ’еҪ’пјҢдҪҶйҖ»иҫ‘еӨҚжқӮеәҰеўһеҠ дәҶпјҢзү№еҲ«жҳҜеңЁз®ЎзҗҶзҲ¶иҠӮзӮ№е’ҢеӯҗиҠӮзӮ№е…ізі»ж—¶гҖӮеҜ№дәҺдәҢеҸүж ‘зҡ„дҝ®ж”№ж“ҚдҪңпјҢйҖ’еҪ’ж–№жі•йҖҡеёёжӣҙдёәзӣҙи§Ӯе’Ңжҳ“дәҺзҗҶи§ЈгҖӮ
е°ҶжңүеәҸж•°з»„иҪ¬жҚўдёәдәҢеҸүжҗңзҙўж ‘
Key Points
еҲҶиҖҢжІ»д№Ӣзҡ„зӯ–з•ҘпјҡйҖүеҸ–дёӯй—ҙе…ғзҙ дҪңдёәж №иҠӮзӮ№пјҢ然еҗҺеҜ№е·ҰеҸіеӯҗж•°з»„еҲҶеҲ«жү§иЎҢеҗҢж ·зҡ„ж“ҚдҪң
зӣёе…ійўҳзӣ®
108е°ҶжңүеәҸж•°з»„иҪ¬жҚўдёәдәҢеҸүжҗңзҙўж ‘
и§Ҷйў‘и®Іи§Ј
жһ„йҖ е№іиЎЎдәҢеҸүжҗңзҙўж ‘
йҮҚзӮ№еҲҶжһҗ
е…ій”®еңЁдәҺжҜҸж¬ЎйғҪиҰҒйҖүеҸ–ж•°з»„дёӯй—ҙзҡ„е…ғзҙ дҪңдёәж ‘зҡ„ж №иҠӮзӮ№пјҢиҝҷж ·еҸҜд»ҘзЎ®дҝқж ‘зҡ„е·ҰеҸідёӨиҫ№дҝқжҢҒе№іиЎЎгҖӮ
ж–№жі•дёҖпјҡйҖ’еҪ’жі•
def sortedArrayToBST(nums): if not nums: return None mid = len(nums) // 2 root_val = nums[mid] root = TreeNode(root_val) root.left = sortedArrayToBST(nums[:mid]) root.right = sortedArrayToBST(nums[mid+1:]) return rootж–№жі•дәҢпјҡиҝӯд»Јжі•
def sortedArrayToBST(nums): if not nums: return None # з”ЁдәҺдҝқеӯҳеӨ„зҗҶиҠӮзӮ№зҡ„ж Ҳ node_stack = [] # з”ЁдәҺдҝқеӯҳж•°з»„иҢғеӣҙзҡ„ж Ҳ range_stack = [(0, len(nums) - 1)] # еҲӣе»әдёҖдёӘиҷҡжӢҹзҡ„ж №иҠӮзӮ№ root = TreeNode(0) node_stack.append((root, True)) while range_stack: left, right = range_stack.pop() parent, is_left = node_stack.pop() if left > right: continue mid = (left + right) // 2 # еҲӣе»әеҪ“еүҚиҠӮзӮ№ current_node = TreeNode(nums[mid]) # е°ҶеҪ“еүҚиҠӮзӮ№иҝһжҺҘеҲ°зҲ¶иҠӮзӮ№ if is_left: parent.left = current_node else: parent.right = current_node # еӨ„зҗҶе·Ұеӯҗж ‘ node_stack.append((current_node, True)) range_stack.append((left, mid - 1)) # еӨ„зҗҶеҸіеӯҗж ‘ node_stack.append((current_node, False)) range_stack.append((mid + 1, right)) return root.leftжҠҠдәҢеҸүжҗңзҙўж ‘иҪ¬жҚўдёәзҙҜеҠ ж ‘
Key Points
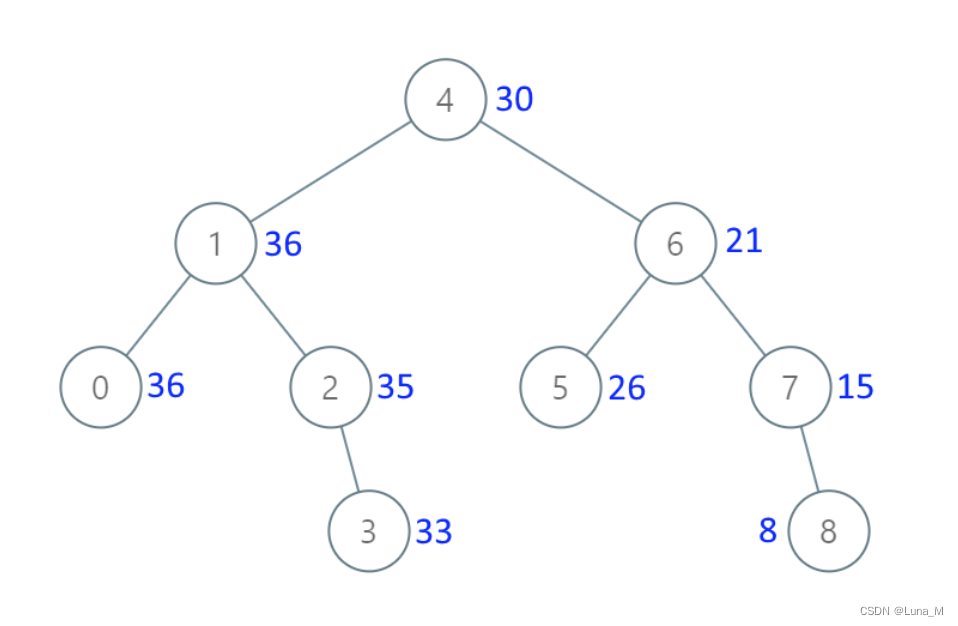
з»ҷеҮәдәҢеҸү жҗңзҙў ж ‘зҡ„ж №иҠӮзӮ№пјҢиҜҘж ‘зҡ„иҠӮзӮ№еҖјеҗ„дёҚзӣёеҗҢпјҢиҜ·дҪ е°Ҷе…¶иҪ¬жҚўдёәзҙҜеҠ ж ‘пјҲGreater Sum TreeпјүпјҢдҪҝжҜҸдёӘиҠӮзӮ№ node зҡ„ж–°еҖјзӯүдәҺеҺҹж ‘дёӯеӨ§дәҺжҲ–зӯүдәҺ node.val зҡ„еҖјд№Ӣе’ҢгҖӮ
зӣёе…ійўҳзӣ®
538. жҠҠдәҢеҸүжҗңзҙўж ‘иҪ¬жҚўдёәзҙҜеҠ ж ‘
и§Ҷйў‘и®Іи§Ј
дәҢеҸүж ‘е®Ңз»“
йҮҚзӮ№еҲҶжһҗ
ж–№жі•дёҖпјҡйҖ’еҪ’жі•
class Solution(object): def __init__(self): self.sum_value = 0 def convertBST(self, root): """ :type root: TreeNode :rtype: TreeNode """ if not root: return root root.right = self.convertBST(root.right) self.sum_value += root.val root.val = self.sum_value root.left = self.convertBST(root.left) return rootж–№жі•дәҢпјҡиҝӯд»Јжі• еҸҚеҗ‘дёӯеәҸйҒҚеҺҶ
жҢүз…§еҸҚеҗ‘дёӯеәҸйҒҚеҺҶпјҲеҸі->иҠӮзӮ№->е·Ұпјүзҡ„йЎәеәҸпјҢдҪҝз”Ёж ҲжқҘиҝӯд»Јең°йҒҚеҺҶж ‘
def convertBST(root): if not root: return root current = root stack = [] sum_value = 0 while current or stack: # е°ҶеҪ“еүҚиҠӮзӮ№еҸҠе…¶жүҖжңүеҸіеӯҗиҠӮзӮ№еҺӢе…Ҙж Ҳ while current: stack.append(current) current = current.right current = stack.pop() # и®ҝй—®ж ҲйЎ¶е…ғзҙ пјҲеҪ“еүҚжңҖеӨ§иҠӮзӮ№пјү sum_value += current.val current.val = sum_value current = current.left # иҪ¬еҗ‘е·Ұеӯҗж ‘ return rootж–№жі•дәҢпјҡиҝӯд»Јжі• з»ҹдёҖиҝӯд»Јжі•пјҲйўңиүІж Үи®°пјү
иҜҰи§Ғ python coding with ChatGPT жү“еҚЎз¬¬13еӨ©| дәҢеҸүж ‘зҡ„ж·ұеәҰдјҳе…ҲйҒҚеҺҶ дёӯзҡ„иҝӯд»ЈйҒҚеҺҶ жӢ“еұ• з»ҹдёҖзҡ„иҝӯд»Јжі•
def convertBST(root): if not root: return root WHITE = 0 # дҪҝз”ЁеёёйҮҸжқҘжҸҗй«ҳд»Јз ҒеҸҜиҜ»жҖ§ GREY = 1 stack = [(root, WHITE)] sum_value = 0 # зҙҜеҠ еҸҳйҮҸпјҢз”ЁдәҺжӣҙж–°иҠӮзӮ№зҡ„еҖј while stack: node, color = stack.pop() if color == WHITE: # иҠӮзӮ№йҰ–ж¬Ўи®ҝй—®пјҢе…ҲеӨ„зҗҶеҸіеӯҗиҠӮзӮ№ stack.append((node, GREY)) if node.right: stack.append((node.right, WHITE)) else: # иҠӮзӮ№з¬¬дәҢж¬Ўи®ҝй—®пјҢжӣҙж–°иҠӮзӮ№еҖје№¶еӨ„зҗҶе·ҰеӯҗиҠӮзӮ№ sum_value += node.val node.val = sum_value if node.left: stack.append((node.left, WHITE)) return rootGPT4зӮ№иҜ„пјҡ
зӣёе…ійҳ…иҜ»пјҡ
1гҖҒVPSжҢӮжңәе…Ҙй—Ёз§ҳзұҚпјҢж•ҲзӣҠжңҖеӨ§еҢ–пјҢиҪ»жқҫдёҠжүӢж“ҚдҪңжҢҮеҚ—
2гҖҒVPSеҹҹеҗҚзҷҪеҗҚеҚ•пјҢе®үе…Ёй…ҚзҪ®иҜҰи§ЈдёҺж“ҚдҪңжҢҮеҚ—
3гҖҒзӢ¬е®¶жҸӯз§ҳпјҢж–°еҠ еқЎVPSдёҚйҷҗжөҒйҮҸдҪҝз”Ёе®қе…ёпјҒ
4гҖҒй«ҳж•Ҳ64m VPS ***дҪҝз”Ёз§ҳзұҚеӨ§жҸӯз§ҳпјҢдёҖзҪ‘жү“е°ҪжүҖжңүж“ҚдҪңжҢҮеҚ—пјҒ
5гҖҒVPSз®ЎзҗҶжҺ§еҲ¶еҸ°пјҢдә‘з«Ҝзӣ‘жҺ§зҡ„дёҖз«ҷејҸж“ҚдҪңдҪ“йӘҢ