Java 【数据结构】 TreeSet&TreeMap（二叉搜索树详解）【神装】

登神长阶

 第八神装 TreeSet

   第九神装  TreeMap

目录

💉 一.二叉搜索树

🩸1. 定义

💊2. 基本操作

🩹3. 插入操作

🩼4. 查找操作

🩺5. 删除操作*

🩻6. 遍历操作

🪒7.性能分析

🪥二.TreeSet

🧽1. 定义

🧻 2.操作

🪣3. Set主要特性

🫧4. TreeSet的内部实现

🛒5. 应用场景

🧯三.TreeMap

🧹1.定义

🪤2.操作

🧷3.Map的主要特性

🧿4. TreeMap的内部实现

🪬5.应用场景 

🗿四.总结与反思

💉 一.二叉搜索树

首先我们要知道TreeSet/TreeMap底层都采用的都是一种二叉搜索树（也叫自平衡二叉树），因此我们先来了解一下二叉搜索树。

对于他的学习若之前没有了解的可以参考：Java 【数据结构】 二叉树（Binary_Tree）【神装】

🩸1. 定义

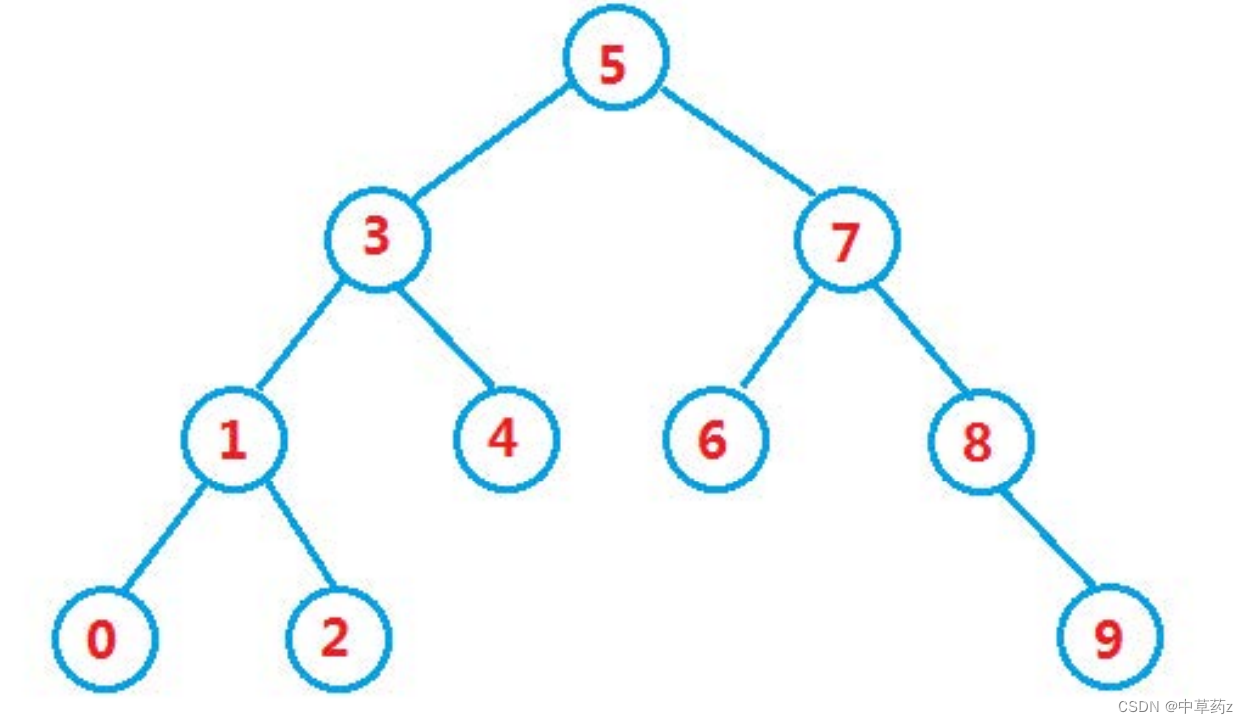
二叉搜索树（Binary Search Tree，简称BST），是一种特殊的二叉树，它具有以下性质：

• 每个节点都有一个键（Key）和两个指向其他节点的指针（左子指针和右子指针）。
• 任意节点的左子树中的所有键都小于该节点的键。
• 任意节点的右子树中的所有键都大于该节点的键。
• 左右子树也都是二叉搜索树。
• 不存在键值相等的节点。

  

  在Java中，我们可以这样定义一个二叉搜索树：

  public class BinarySearchTree {
      private class Node {
          int val;
          Node left;
          Node right;
          
          Node(int val) {
              this.val = val;
              left = null;
              right = null;
          }
      }
      
      private Node root;
      
      // 构造函数、插入方法、查找方法、删除方法等...
  }
  

  💊2. 基本操作

  二叉搜索树支持以下基本操作：

  • 插入（Insert）：向树中插入一个新节点，保持树的二叉搜索性质。
  • 查找（Search）：在树中查找一个特定的节点。
  • 删除（Delete）：从树中删除一个节点，并保持树的二叉搜索性质。
  • 遍历（Traverse）：对树进行遍历，常用的遍历方式有前序、中序和后序遍历。

    接下来我们详细介绍一下它的各个操作，因为后续二叉树本身是数据结构中一个很关键的知识点，像红黑树，AVL树等等，我们需要牢牢掌握！

    🩹3. 插入操作

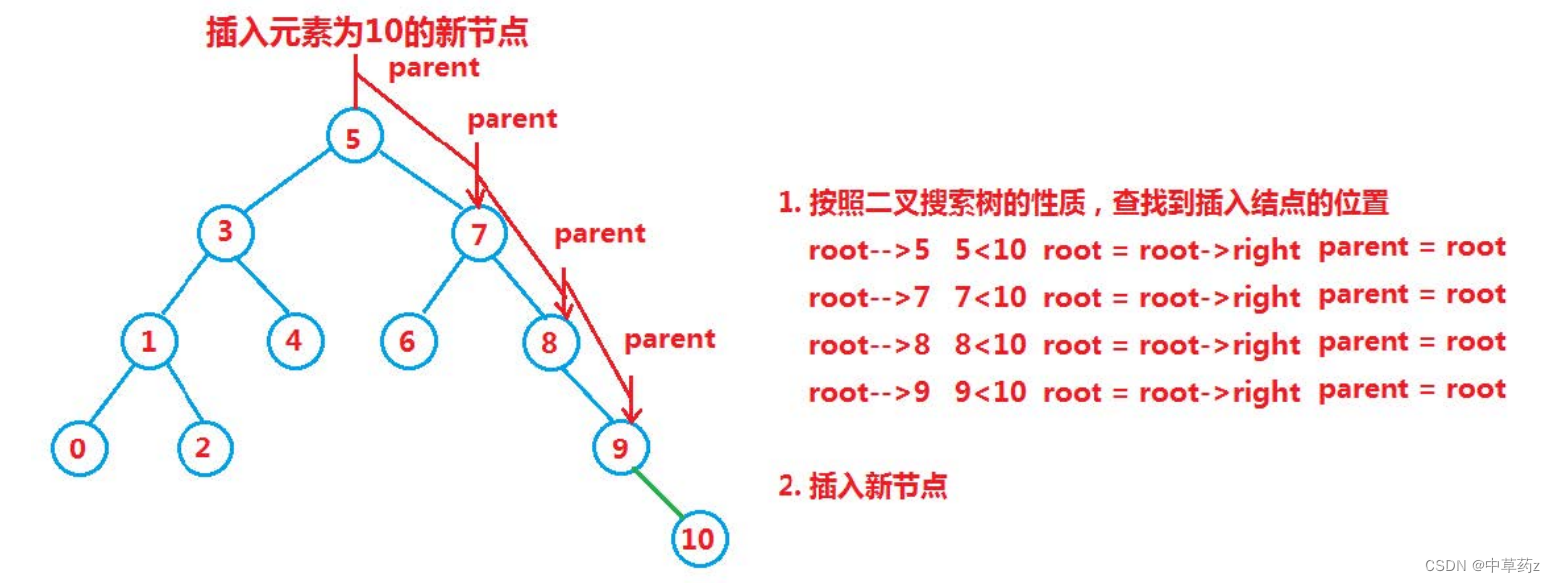
    插入操作的步骤如下：

    1. 创建新节点。
    2. 比较新节点的键与根节点的键：
       • 如果新节点的键小于根节点的键，则将新节点插入到根节点的左子树中。
       • 如果新节点的键大于根节点的键，则将新节点插入到根节点的右子树中。
    3. 如果插入点是空，则直接在新位置插入新节点。
    4. 如果插入点非空，则递归地在相应子树中进行插入操作。

    

    代码: 

     /**
         * 插入一个元素
         * @param key
         */
        public void insert(int key) {
            TreeNode node=new TreeNode(key);
            //若该搜索树为空，则直接作为根节点；
            if (root==null){
                root=node;
            }
            TreeNode cur=root;
            TreeNode parent=null;
            while(cur!=null){
                if (cur.keykey){
                    parent = cur;
                    cur=cur.left;
                }else{
                    return ;
                }
            }
            if (parent.key>key){
                parent.left=node;
            }else{
                parent.right=node;
            }
        }

    🩼4. 查找操作

    查找操作的步骤如下：

    1. 从根节点开始比较。
    2. 如果查找的键小于当前节点的键，则递归地在左子树中查找。
    3. 如果查找的键大于当前节点的键，则递归地在右子树中查找。
    4. 如果找到节点，则返回该节点。
    5. 如果没有找到，则返回null。

    

    代码

     //查找key是否存在
        public TreeNode search(int key) {
            TreeNode cur =root;
            while(cur!=null){
                if (cur.keykey){
                    cur=cur.left;
                }else{
                    return cur;
                }
            }
            return null;
        }

    🩺5. 删除操作*

    设待删除结点为 cur, 待删除结点的双亲结点为 parent 1. cur.left == null
    1. cur 是 root，则 root = cur.right
    2. cur 不是 root，cur 是 parent.left，则 parent.left = cur.right
    3. cur 不是 root，cur 是 parent.right，则 parent.right = cur.right
    2. cur.right == null
    1. cur 是 root，则 root = cur.left
    2. cur 不是 root，cur 是 parent.left，则 parent.left = cur.left
    3. cur 不是 root，cur 是 parent.right，则 parent.right = cur.left
    3. cur.left != null && cur.right != null
    • 需要使用替换法进行删除，即在它的右子树中寻找中序下的第一个结点(关键码最小)，用它的值填补到被删除节点中，再来处理该结点的删除问题

      代码

      //删除key的值
          public boolean remove(int key) {
              TreeNode cur =root;
              TreeNode parent=null;
              while(cur!=null){
                  if (cur.key>key){
                      parent=cur;
                      cur=cur.left;
                  }else if (cur.key