堆排序（c语言）

文章目录

• 前言
• 一.什么是堆
• 二.向下调整算法
• 三.堆排序的创建
• 总结

  ---

  前言

  堆排序（Heapsort）是指利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构，并同时满足堆积的性质：即子结点的键值或索引总是小于（或者大于）它的父节点。

  ---

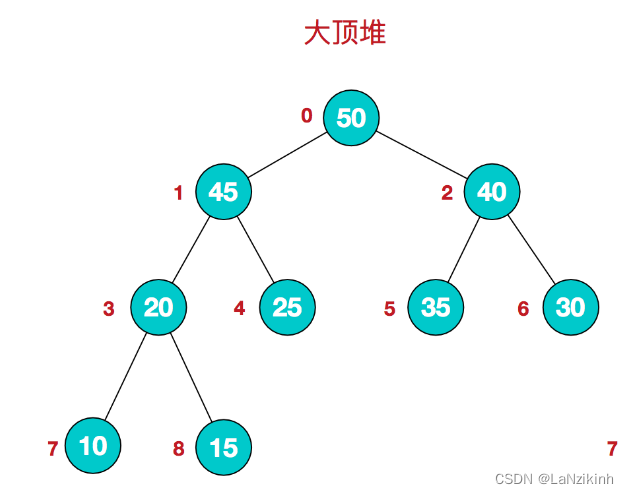
  一.什么是堆

  

  堆它分两种结构逻辑结构和物理结构

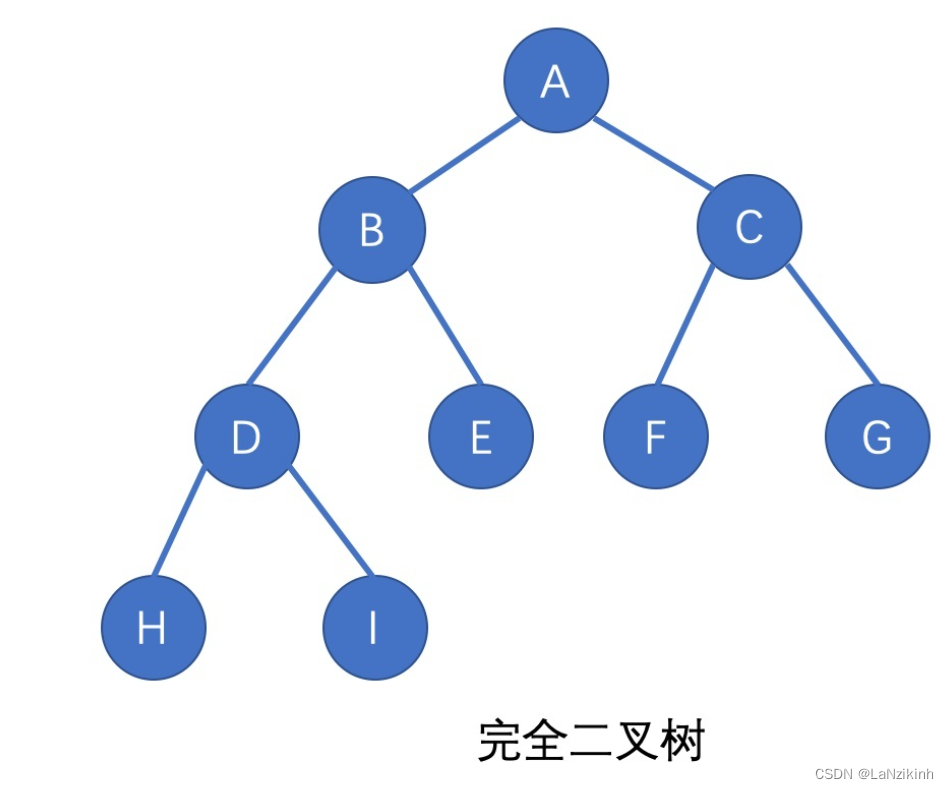
  逻辑结构是完全二叉树

  

  物理结构是数组

  

  堆还有两种特征

  1.结构性：用数组表示的完全二叉树。

  2.有序性：任一结点的根要大于或小于子节点：称为大堆小堆

  通过向标建立父子节点的关系

  左孩子（默认为child）

  leftchild=parent*2+1

  rightchild=parent*2+2

  parent=(child-1)/2

  二.向下调整算法

  要想实现堆排序，首先必须知道什么是向下调整算法。

  前提：左右子树都是小堆或者大堆

  思路：从根节点开始，选出左右孩子中小的那一个，跟父亲比较，如果父亲小就交换，然后再往下调调到叶子节点结束

  

  void AdjustDwon(int* a, int n, int root)
  {
  	int parent = root;
  	 //默认左孩子为child
  	int child = parent * 2 + 1;
  	//不能越界，所以要小于n，因为下标最高到n-1，随意当迟来的当n是出while语句
  	while (child  
  三.堆排序的创建
   
  建堆
   
  就是先把数组转化为堆
   
   
   
  利用向下调整算法去建立堆
   
   
   
  思路：叶子是不用排的，从倒数最后一个非叶子的父亲开始调
   
   
  	//int i = (n - 1 - 1)父亲公式
  	for (int i = (n - 1 - 1) / 2; i >= 0; i--)
  	{
  		AdjustDwon(a, n, i);
  	}
   
  思考：排一个升序是建大堆还是小堆
   
  如果是排小堆的化，每次从头顶拿出数据，就要打乱一个堆，又要把一个堆重新排，他的时间复杂度就为O（N*N),所以要用大堆排，第一个和最后一个交换，把它不看作堆里面的前N -1个数向下调整，选出最大的数再跟倒数第二个位置交换这样它的时间复杂度就为O（N*logN)。
   
  void Heapsort(int* a, int n);
  {
  	//int i = (n - 1 - 1)父亲公式
  	for (int i = (n - 1 - 1) / 2; i >= 0; i--)
  	{
  		AdjustDwon(a, n, i);
  	}
  	
  	int end = n - 1;
  	while (end > 0)
  	{
  		Swap(&a[0], &a[end]);
  		AdjustDwon(a, end, 0);
  		end--;
  	}
  }
   
  四.堆的时间复杂度
   
   
   
  总结
   
    堆是一种很好做调整的结构，在算法题里面使用频度很高。常用于想知道最大值或最小值的情况，比如优先级队列，作业调度等场景。