MATLAB实现高通滤波(附完整代码)
1.MATLAB实现高通滤波器
以下是一个使用MATLAB实现高通滤波器的例子。在这个例子中,我们将设计一个简单的数字高通滤波器,然后将其应用到一个包含低频和高频成分的信号上。
clc;close all;clear all;warning off;%清除变量
rand('seed', 500);
randn('seed', 300);
format long g;
% 创建时间向量
t = 0:0.001:1; % 从0到1秒
% 创建包含低频和高频分量的信号
f1 = 5; % 低频分量
f2 = 50; % 高频分量
y = sin(2*pi*f1*t) + sin(2*pi*f2*t);
% 设计高通滤波器
Fs = 1000; % 采样频率
Fc = 30; % 截止频率
[b, a] = butter(6, Fc/(Fs/2), 'high'); % 6阶Butterworth高通滤波器
% 应用高通滤波器
y_filtered = filter(b, a, y);
% 画出原始信号和滤波后的信号
figure;
subplot(2,1,1);
plot(t, y);
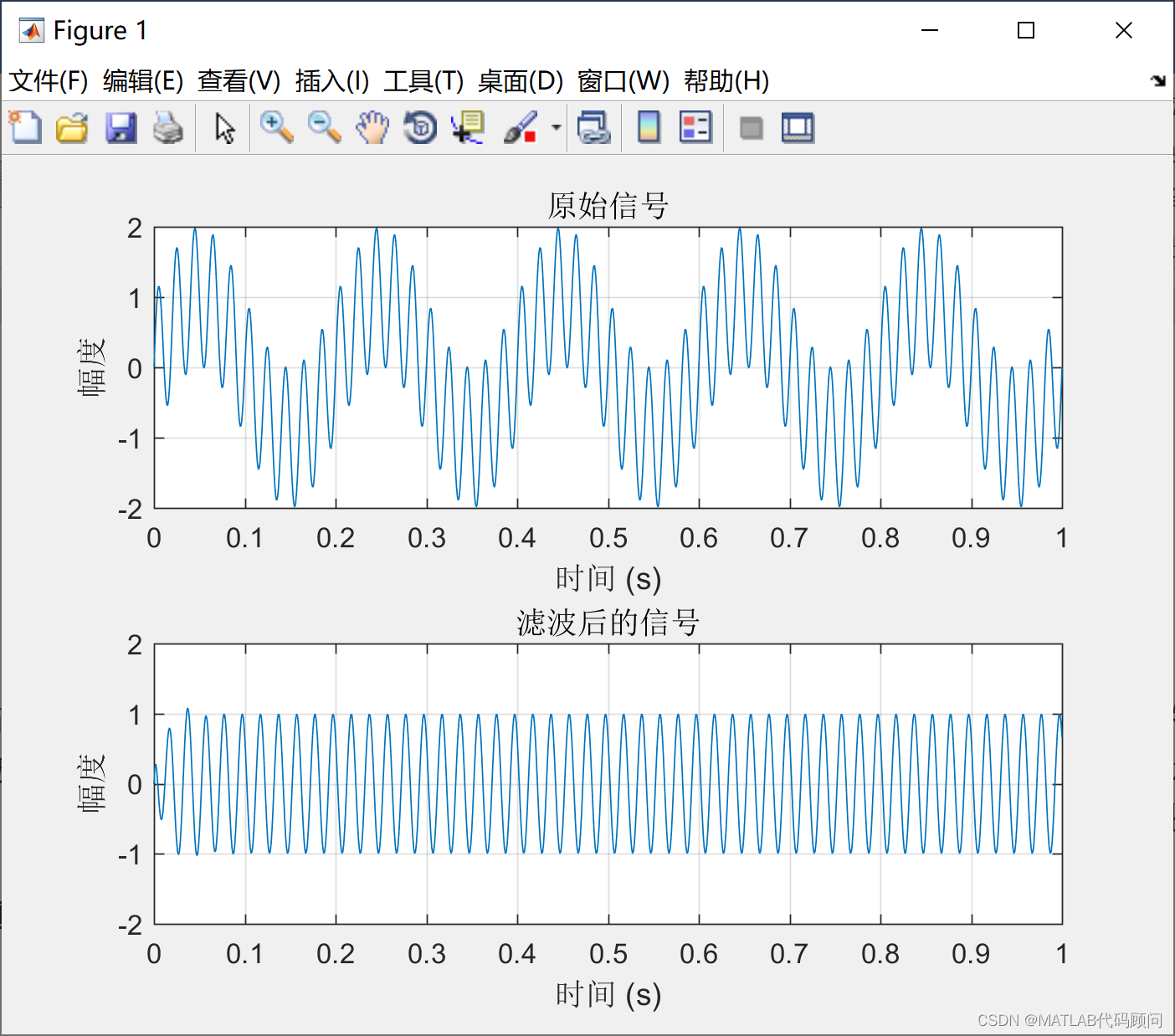
title('原始信号');
xlabel('时间 (s)');
ylabel('幅度');
grid on;
subplot(2,1,2);
plot(t, y_filtered);
title('滤波后的信号');
xlabel('时间 (s)');
ylabel('幅度');
grid on;
此代码首先创建了一个含有5Hz和50Hz成分的信号,然后设计了一个30Hz截止频率的高通滤波器,最后将滤波器应用到信号上。你可以看到,滤波后的信号主要保留了高频(50Hz)成分,而低频(5Hz)成分被滤掉了。你可以试着改变截止频率Fc,看看滤波效果如何变化。
2.高通滤波理论
高通滤波器是一种电子滤波器,它可以通过高频信号,而阻止低于特定截止频率的信号。高通滤波器主要用于消除信号中的低频噪声,或者从广频信号中提取高频成分。
高通滤波器的原理:
高通滤波器的工作原理是基于信号的频率特性。高频信号和低频信号在电路中的行为是不同的。低频信号更容易通过电容,而高频信号更容易通过电感。通过巧妙地组合电阻、电容和电感,可以创建出只允许高频信号通过的电路,这就是高通滤波器。
在数字信号处理中,高通滤波器通常基于傅里叶变换的原理。傅里叶变换可以将信号从时域转换到频域,在频域中可以很容易地识别和操作信号的频率成分。一个简单的数字高通滤波器可能就是将频域中的低频成分设为零,然后再转换回时域。
实现高通滤波器的步骤:
定义滤波器的规格:这包括截止频率,以及滤波器的类型(如Butterworth、Chebyshev等)。
设计滤波器:根据滤波器的规格,计算滤波器的参数。在模拟电路中,这可能涉及到电阻、电容和电感的计算;在数字信号处理中,这通常涉及到滤波器系数的计算。
应用滤波器:将滤波器应用到信号上。在模拟电路中,这可能涉及到电路的搭建;在数字信号处理中,这通常涉及到卷积或其他信号处理算法。
例如,在MATLAB中,你可以使用butter函数来设计一个Butterworth高通滤波器,然后使用filter函数将滤波器应用到信号上。
高通滤波器是信号处理中的重要工具,它们在许多应用中都有用到,包括音频处理、图像处理、通信系统等。