【数值分析——插值法】牛顿插值多项式及Matlab实现

2024-06-04 7247阅读

牛顿多项式插值法（Newton polynomial interpolation）

算法思想及公式定义
对于要插值的数据点，如果是只存在一对数据点，即 ( x 0 , y 0 ) \left(x_{0},y_{0}\right) (x0,y0) ，那么插值多项式显然为：
f 0 ( x ) = y 0 f_{0}\left(x\right)=y_{0} f0(x)=y0
其中， a 0 = y 0 a_{0}=y_{0} a0=y0

如果现在我们新增一个数据点 ( x 1 , y 1 ) \left(x_{1},y_{1}\right) (x1,y1) ，那么，插值多项式的图像就是经过这两个点 ( x 0 , y 0 ) 、 ( x 1 , y 1 ) \left(x_{0},y_{0}\right)、\left(x_{1},y_{1}\right) (x0,y0)、(x1,y1) 的直线，不难得到插值函数为：
f 1 ( x ) = y 0 + a 1 ⋅ ( x − x 0 ) f_{1}\left(x\right)=y_{0}+a_{1}\cdot \left(x-x_{0}\right) f1(x)=y0+a1⋅(x−x0)
带入 f 1 ( x 1 ) = y 1 f_{1}\left(x_{1}\right)=y_{1} f1(x1)=y1 可得， a 1 = y 1 − y 0 x 1 − x 0 a_{1}=\frac{y_{1}-y_{0}}{x_{1}-x_{0}} a1=x1−x0y1−y0

现在，我们在新增一个数据点 ( x 2 , y 2 ) \left(x_{2},y_{2}\right) (x2,y2) ，还是写成之前的 f 1 ( x ) f_{1}\left(x\right) f1(x) 的形式，即：
f 2 ( x ) = y 0 + y 1 − y 0 x 1 − x 0 ⋅ ( x − x 0 ) + a 2 ⋅ ( x − x 0 ) ⋅ ( x − x 1 ) f_{2}\left(x\right)=y_{0}+\frac{y_{1}-y_{0}}{x_{1}-x_{0}}\cdot \left(x-x_{0}\right)+a_{2}\cdot \left(x-x_{0}\right)\cdot \left(x-x_{1}\right) f2(x)=y0+x1−x0y1−y0⋅(x−x0)+a2⋅(x−x0)⋅(x−x1)
带入 f 2 ( x 2 ) = y 2 f_{2}\left(x_{2}\right)=y_{2} f2(x2)=y2 可得， a 2 = y 2 − y 0 x 2 − x 0 − y 1 − y 0 x 1 − x 0 x 2 − x 1 a_{2}=\frac{\frac{y_{2}-y_{0}}{x_{2}-x_{0}}-\frac{y_{1}-y_{0}}{x_{1}-x_{0}}}{x_{2}-x_{1}} a2=x2−x1x2−x0y2−y0−x1−x0y1−y0

我们可以看到，每增加一个数据点后，我们只需要对之前的插值多项式做一个修正即可，即增加一项。如果我们可以求出 a i a_{i} ai ，那么我们就能求出新增数据点之后的插值多项式。

根据上面的分析，我们定义牛顿插值多项式为：
f n ( x ) = a 0 + a 1 ⋅ ( x − x 0 ) + a 2 ⋅ ( x − x 0 ) ⋅ ( x − x 1 ) + ⋯ + a n ⋅ ( x − x 0 ) ⋅ ( x − x 1 ) ⋯ ( x − x n − 1 ) f_{n}\left(x\right)=a_{0}+a_{1}\cdot \left(x-x_{0}\right)+a_{2}\cdot \left(x-x_{0}\right)\cdot \left(x-x_{1}\right)+\cdots +a_{n}\cdot \left(x-x_{0}\right)\cdot \left(x-x_{1}\right)\cdots \left(x-x_{n-1}\right) fn(x)=a0+a1⋅(x−x0)+a2⋅(x−x0)⋅(x−x1)+⋯+an⋅(x−x0)⋅(x−x1)⋯(x−xn−1)
其中， a n ( n = 0 , 1 , 2 ⋯ n ) a_{n}\left(n=0,1,2\cdots n\right) an(n=0,1,2⋯n) 为待定系数。
商差（均差）的概念及性质
自变量之差与因变量之差叫做商差，函数 y = f ( x ) y=f\left(x\right) y=f(x) 在区间 [ x i , x i + 1 ] \left[x_{i},x_{i+1}\right] [xi,xi+1] 的平均变化率：
f [ x i , x i + 1 ] = f ( x i + 1 ) − f ( x i ) x i + 1 − x i f\left[x_{i},x_{i+1}\right]=\frac{f\left(x_{i+1}\right)-f\left(x_{i}\right)}{x_{i+1}-x_{i}} f[xi,xi+1]=xi+1−xif(xi+1)−f(xi)
称为 f ( x ) f\left(x\right) f(x) 关于 x i , x i + 1 x_{i},x_{i+1} xi,xi+1 的一阶差商，并记为 f [ x i , x i + 1 ] f\left[x_{i},x_{i+1}\right] f[xi,xi+1] 。

同理可得，二阶商差为：
f [ x i , x i + 1 , x i + 2 ] = f [ x i + 1 , x i + 2 ] − f [ x i , x i + 1 ] x i + 2 − x i f\left[x_{i},x_{i+1},x_{i+2}\right]=\frac{f\left[x_{i+1},x_{i+2}\right]-f\left[x_{i},x_{i+1}\right]}{x_{i+2}-x_{i}} f[xi,xi+1,xi+2]=xi+2−xif[xi+1,xi+2]−f[xi,xi+1]
⋮ \vdots ⋮
m阶商差为：
f [ x 0 , x 1 , x 2 , ⋯ , x m ] = f [ x 1 , x 2 , ⋯ , x m ] − f [ x 0 , x 1 , ⋯ , x m − 1 ] x m − x 0 f\left[x_{0},x_{1},x_{2},\cdots,x_{m}\right]=\frac{f\left[x_{1},x_{2},\cdots,x_{m}\right]-f\left[x_{0},x_{1},\cdots,x_{m-1}\right]}{x_{m}-x_{0}} f[x0,x1,x2,⋯,xm]=xm−x0f[x1,x2,⋯,xm]−f[x0,x1,⋯,xm−1]

商差表

x i x_{i} xi	f ( x i ) f\left(x_{i}\right) f(xi)	f [ x i , x i + 1 ] f\left[x_{i},x_{i+1}\right] f[xi,xi+1]	f [ x i , x i + 1 , x i + 2 ] f\left[x_{i},x_{i+1},x_{i+2}\right] f[xi,xi+1,xi+2]	f [ x i , x i + 1 , x i + 2 , x i + 3 ] f\left[x_{i},x_{i+1},x_{i+2},x_{i+3}\right] f[xi,xi+1,xi+2,xi+3]	⋯ \cdots ⋯
x 0 x_{0} x0	f ( x 0 ) f\left(x_{0}\right) f(x0)	-	-	-	⋯ \cdots ⋯
x 1 x_{1} x1	f ( x 1 ) f\left(x_{1}\right) f(x1)	f [ x 0 , x 1 ] f\left[x_{0},x_{1}\right] f[x0,x1]	-	-	⋯ \cdots ⋯
x 2 x_{2} x2	f ( x 2 ) f\left(x_{2}\right) f(x2)	f [ x 1 , x 2 ] f\left[x_{1},x_{2}\right] f[x1,x2]	f [ x 0 , x 1 , x 2 ] f\left[x_{0},x_{1},x_{2}\right] f[x0,x1,x2]	-	⋯ \cdots ⋯
x 3 x_{3} x3	f ( x 3 ) f\left(x_{3}\right) f(x3)	f [ x 2 , x 3 ] f\left[x_{2},x_{3}\right] f[x2,x3]	f [ x 1 , x 2 , x 3 ] f\left[x_{1},x_{2},x_{3}\right] f[x1,x2,x3]	f [ x 0 , x 1 , x 2 , x 3 ] f\left[x_{0},x_{1},x_{2},x_{3}\right] f[x0,x1,x2,x3]	⋯ \cdots ⋯
⋮ \vdots ⋮	⋮ \vdots ⋮	⋮ \vdots ⋮	⋮ \vdots ⋮	⋮ \vdots ⋮	⋱ \ddots ⋱

插值余项
定义：若在 [ a , b ] \left[a,b\right] [a,b] 上用 L n ( x ) L_{n}\left(x\right) Ln(x) 近似 f ( x ) f\left(x\right) f(x) ，则其截断误差为 R n ( x ) = f ( x ) − L n ( x ) R_{n}\left(x\right)=f\left(x\right)-L_{n}\left(x\right) Rn(x)=f(x)−Ln(x) ，也称为插值多项式的余项。
- 牛顿插值多项式的余项
  根据均差的定义：
  f [ x 0 , x 1 , x 2 , ⋯ , x m ] = f [ x 1 , x 2 , ⋯ , x m ] − f [ x 0 , x 1 , ⋯ , x m − 1 ] x m − x 0 f\left[x_{0},x_{1},x_{2},\cdots,x_{m}\right]=\frac{f\left[x_{1},x_{2},\cdots,x_{m}\right]-f\left[x_{0},x_{1},\cdots,x_{m-1}\right]}{x_{m}-x_{0}} f[x0,x1,x2,⋯,xm]=xm−x0f[x1,x2,⋯,xm]−f[x0,x1,⋯,xm−1]
  有
  f [ x , x 0 , x 1 , ⋯ , x m − 1 ] = f [ x 0 , x 1 , x 2 , ⋯ , x m ] + f [ x , x 0 , x 1 , ⋯ , x m ] ⋅ ( x − x m ) f\left[x,x_{0},x_{1},\cdots,x_{m-1}\right]=f\left[x_{0},x_{1},x_{2},\cdots,x_{m}\right]+f\left[x,x_{0},x_{1},\cdots,x_{m}\right]\cdot \left(x-x_{m}\right) f[x,x0,x1,⋯,xm−1]=f[x0,x1,x2,⋯,xm]+f[x,x0,x1,⋯,xm]⋅(x−xm)
  ⋮ \vdots ⋮
  f [ x , x 0 ] = f [ x 0 , x 1 ] + f [ x , x 0 , x 1 ] ⋅ ( x − x 1 ) f\left[x,x_{0}\right]=f\left[x_{0},x_{1}\right]+f\left[x,x_{0},x_{1}\right]\cdot \left(x-x_{1}\right) f[x,x0]=f[x0,x1]+f[x,x0,x1]⋅(x−x1)
  f ( x ) = f ( x 0 ) + f [ x , x 0 ] ⋅ ( x − x 0 ) f\left(x\right)=f\left(x_{0}\right)+f\left[x,x_{0}\right]\cdot \left(x-x_{0}\right) f(x)=f(x0)+f[x,x0]⋅(x−x0)
  把前一式代入后一式中，就可以得到：
  f ( x ) = f ( x 0 ) + f [ x , x 0 ] ⋅ ( x − x 0 ) + f [ x , x 0 , x 1 ] ⋅ ( x − x 0 ) ⋅ ( x − x 1 ) + ⋯ + f [ x 0 , x 1 , ⋯ , x n ] ⋅ ( x − x 0 ) ⋯ ( x − x n − 1 ) + f [ x , x 0 , x 1 , ⋯ , x n ] ⋅ w n + 1 ( x ) f\left(x\right)=f\left(x_{0}\right)+f\left[x,x_{0}\right]\cdot \left(x-x_{0}\right)+f\left[x,x_{0},x_{1}\right]\cdot \left(x-x_{0}\right)\cdot\left(x-x_{1}\right)+\cdots +f\left[x_{0},x_{1},\cdots,x_{n}\right]\cdot \left(x-x_{0}\right)\cdots \left(x-x_{n-1}\right)+f\left[x,x_{0},x_{1},\cdots,x_{n}\right]\cdot w_{n+1}\left(x\right) f(x)=f(x0)+f[x,x0]⋅(x−x0)+f[x,x0,x1]⋅(x−x0)⋅(x−x1)+⋯+f[x0,x1,⋯,xn]⋅(x−x0)⋯(x−xn−1)+f[x,x0,x1,⋯,xn]⋅wn+1(x)
  其中，
  P n [ x ] = f ( x 0 ) + f [ x , x 0 ] ⋅ ( x − x 0 ) + f [ x , x 0 , x 1 ] ⋅ ( x − x 0 ) ⋅ ( x − x 1 ) + ⋯ + f [ x 0 , x 1 , ⋯ , x n ] ⋅ ( x − x 0 ) ⋯ ( x − x n − 1 ) P_{n}\left[x\right]=f\left(x_{0}\right)+f\left[x,x_{0}\right]\cdot \left(x-x_{0}\right)+f\left[x,x_{0},x_{1}\right]\cdot \left(x-x_{0}\right)\cdot\left(x-x_{1}\right)+\cdots +f\left[x_{0},x_{1},\cdots,x_{n}\right]\cdot \left(x-x_{0}\right)\cdots \left(x-x_{n-1}\right) Pn[x]=f(x0)+f[x,x0]⋅(x−x0)+f[x,x0,x1]⋅(x−x0)⋅(x−x1)+⋯+f[x0,x1,⋯,xn]⋅(x−x0)⋯(x−xn−1)
  w n + 1 ( x ) = ( x − x 0 ) ⋅ ( x − x 1 ) ⋯ ( x − x n ) w_{n+1}\left(x\right)=\left(x-x_{0}\right)\cdot \left(x-x_{1}\right)\cdots \left(x-x_{n}\right) wn+1(x)=(x−x0)⋅(x−x1)⋯(x−xn)
  P n ( x ) P_{n}\left(x\right) Pn(x) 是近似 f ( x ) f\left(x\right) f(x) 的插值多项式，前面也推导出了
  f ( x ) = P n ( x ) + R n ( x ) f\left(x\right)=P_{n}\left(x\right)+R_{n}\left(x\right) f(x)=Pn(x)+Rn(x)
  所以有
  f ( x ) − P n ( x ) = R n ( x ) f\left(x\right)-P_{n}\left(x\right)=R_{n}\left(x\right) f(x)−Pn(x)=Rn(x)
  那么插值余项为：
  R n ( x ) = f [ x , x 0 , x 1 , ⋯ , x n ] ⋅ w n + 1 ( x ) R_{n}\left(x\right)=f\left[x,x_{0},x_{1},\cdots,x_{n}\right]\cdot w_{n+1}\left(x\right) Rn(x)=f[x,x0,x1,⋯,xn]⋅wn+1(x)
- Matlab实现（只实现了插值函数，测试函数同前面的拉格朗日插值的测试）
```
function y=newton(x0,y0,x)
%   Newton插值函数
%   x0为已知数据点的x坐标
%   y0为已知数据点的y坐标
%   x为插值点的x坐标
%   y为各插值点函数值
% 获取数据点的个数
n=length(x0);
% 判断输入信息x0和y0的信息正确
if n~=length(y0)
    error('维数不等');
else
% 获取要预测插值点的个数
m=length(x);
% 初始化y值，并幅值为0，向量维度为m
y=zeros(1,m);
% 初始化A-->代表均差表，可参考均差表的形式来理解代码的实现
A=zeros(n,n);
A(:,1)=y0;
for j=2:n
    for i=j:n
        A(i,j)=(A(i,j-1)-A(i-1,j-1))/(x0(i)-x0(i-j+1));
    end
end
% 求整个插值函数
for i=1:n
    % 定义中间变量p
    p=1.0;
    for j=1:i-1
        p=p.*(x-x0(j));
    end
    y=y+A(i,i)*p;
end
end
```
  - 关于代码中A矩阵实现的由来
  - 结果分析
    根据原理分析，牛顿插值多项式是插值多项式 P ( x ) P\left(x\right) P(x) 的另一种表示形式，与Lagrange多项式相比，它不仅克服了增加一个节点时整个计算工作重新开始的缺点, 且可以节省乘除法运算次数。
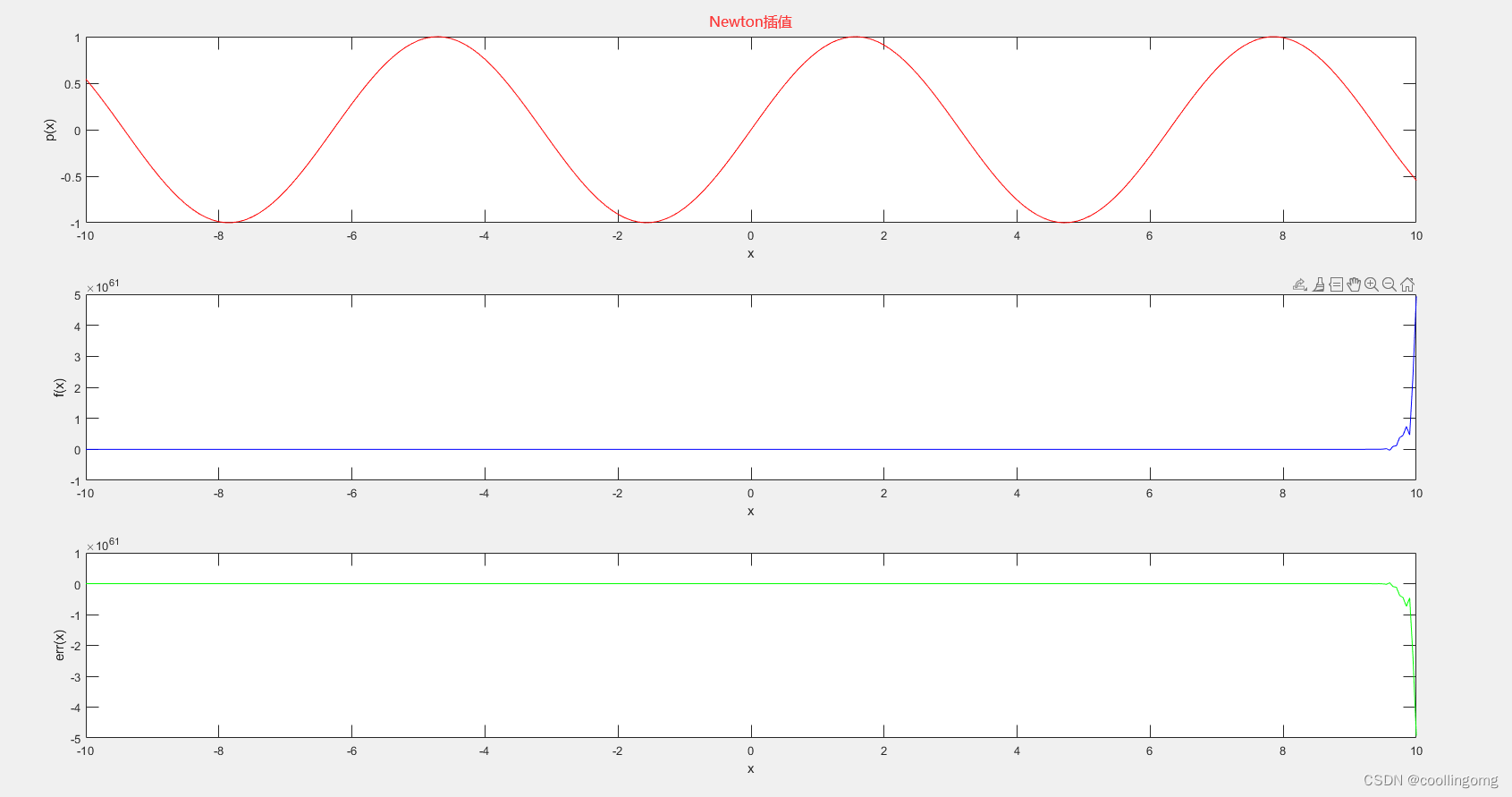
    - Matlab对于sin函数的插值结果
      
      但是根据Matlab实现的计算结果来看，lagrange插值和newton插值的结果并不一样，这和之前推导出来的唯一性相违背，那么到底哪儿应该是正确的呢？为了寻找答案，我翻遍了网上的资料，以及看了我的Matlab代码实现，发现好像都没有什么问题，那么为什么会出现这种问题呢，难道真的是前面的多项式插值的唯一性存在错误吗？
      
      直到我一步步的将前面的实现过程在matlab的命令行敲出来，然后观察每个变量的具体数值的时候发现了如下图所示：
      
      发现了什么，随着不断地计算，后面的项目全部趋近于0，直到全为0。看到这儿，我豁然开朗，这不就是前面提到的（数值分析第一章讲的）截断误差吗！就是这个截断误差，导致了两种插值方法的结果相差这么大！
      
      所以，虽然newton插值每增加一个节点，只需要修正插值多项值得一项，但是，在计算机计算的过程中，其截断误差也会随着项得不断增多而不断得增大。