【C++】从零开始map与set的封装

2024-06-04 1107阅读

【C++】从零开始map与set的封装 第1张

送给大家一句话：

今日的事情，尽心、尽意、尽力去做了，无论成绩如何，都应该高高兴兴地上床恬睡。 – 三毛 《亲爱的三毛》

🌃🌃🌃🌃🌃🌃🌃🌃🌃

🌏🌏🌏🌏🌏🌏🌏🌏🌏

从零开始map与set的封装

  • 1 前言
  • 2 红黑树的迭代器
  • 3 map与set的封装
    • 3.1 红黑树的改进
    • 3.2 map的封装
    • 3.3 set 的封装
    • 4 总结
    • Thanks♪(･ω･)ﾉ谢谢阅读！！！
    • 下一篇文章见！！！

      1 前言

      为了map与set 的封装，我们进行了非常充足的知识储备！！！

      首先，为了了解map 与 set 的底层原理我们开始学习二叉搜索树,二叉搜索树在二叉树的基础上增添了：

      • 若它的左子树不为空，则左子树上所有节点的值都小于根节点的值
      • 若它的右子树不为空，则右子树上所有节点的值都大于根节点的值
      • 它的左右子树也分别为二叉搜索树
      • 注意通常二叉搜索树不会有相同的键值

        这样可以在一定程度上满足高效搜索的需求，但是在极端的情况（单子树情况）其效率会下降到O(n)。因此就有了改进的二叉搜索树：AVL树和红黑树。他们都增加一些特性使其最大程度上近似平衡二叉树！

        AVL 树 和 红黑树 都是在保持二叉搜索树基本性质的基础上，通过旋转和重新平衡等操作，确保树的高度保持在一个相对平衡的状态，从而保证了操作的时间复杂度始终为 O(logn)。它们的出现大大提高了二叉搜索树在实际应用中的性能和稳定性。

        AVL树增加了以下特性：

        • 它的左右子树都是AVL树
        • 左右子树高度之差(简称平衡因子)的绝对值不超过1(-1 / 0 / 1 )

          在平衡因子超出要求就会进行旋转，旋转分为：右单旋 ，左单旋，左右双旋，右左双旋。

          红黑树加入以下特性:

          • ⚠️每个节点要么是红色，要么是黑色。
          • ⚠️根节点必须是黑色的。
          • ⚠️如果一个节点是红色的，则它的两个子节点必须是黑色的。
          • ⚠️对于任意一个节点，从该节点到其所有后代叶子节点的简单路径上，必须包含相同数目的黑色节点。
          • ⚠️每个叶子节点都是黑色的。这里的叶子节点指的是为空的节点。

            在不满足规则时也会进行旋转。但是旋转的频率比AVL树要少很多，红黑树是只是接近平衡，AVL树几乎就是平衡的！

            map与set大多数情况是用来检索的工具，我们底层使用红黑树来完成map与set的封装。

            进行封装之前，我们先来实现一个非常重要的东西：迭代器

            2 红黑树的迭代器

            迭代器的好处是可以方便遍历。如果想要给红黑树增加迭代器，需要考虑以前问题：

            1. 迭代器的框架如何实现，才能满足泛型编程的需求？？
            2. STL明确规定，begin()与end()代表的是一段前闭后开的区间，而对红黑树进行中序遍历后，可以得到一个有序的序列，因此：begin()可以放在红黑树中最小节点(即最左侧节点)的位置，end()放在最大节点(最右侧节点)的下一个位置，这里为了方便就给nullptr。
            3. operator++()与operator–()要如何实现？这里的++和–要满足中序遍历的顺序，就不能简单的进行指针的移动了！

            接下来我们来逐个实现。

            首先我们来搭建一下迭代器的框架

            // 迭代器
//T 表示数据类型 Ref为引用 Ptr为指针
template
struct _RBTreeIterator
{
	//为了方便调用，我们重命名一下
	typedef RBTreeNode Node;
	typedef _RBTreeIterator Self;
	//内部是节点指针
	Node* _node;
	_RBTreeIterator(Node* node)
		:_node(node)
	{}
	//两种指向方式
	Ref operator*()
	{
		return _node->_data;
	}
	Ptr operator&()
	{
		return &_node->_data;
	}
	bool operator!= (const Self& s)
	{
		return _node != s._node;
	}
};

            接下来我们来实现++和–的操作。

            中序遍历的顺序是先遍历左边再遍历当前节点最后是右子树。所以在跌迭代器指向当前节点的时候，说明当前节点的左子树已经遍历完了，如果++，就要去找右边的最左节点。如果没有右子树，说明该节点以下的部分已经遍历完了，接下来要去向上进行，找到是祖先左边的节点：

            //迭代器的++ 中序遍历的顺序
Self& operator++()
{
	//首先，能访问到当前节点说明左子树的都已经访问过啦
	//所以就要分类讨论
	//如果右边有子树,就要去寻找右子树的最左节点
	if (_node->_right)
	{
		Node* cur = _node->_right;
		while (cur->_left)
		{
			cur = cur->_left;
		}
		_node = cur;
	}
	//如果右边没有子树了，说明该节点以下的子树都已遍历完，那么就要向上进行
	//找到祖先节点(注意祖先节点右边还没遍历)
	//此时也要进行分类讨论
	else
	{
		Node* cur = _node;
		Node* parent = _node->_parent;
		//_node == parent->_right
		//说明parent的节点已经访问过了
		while (parent && cur == parent->_right)
		{
			cur = parent;
			parent = cur->_parent;
		}
		_node = parent;
	}
	return *this;
}

            –与++完全相反。

            这样红黑树的迭代器就成功设置好了，我们的红黑树更加完美了！！！

            实现了迭代器接下来我们就来实现map与set的封装

            3 map与set的封装

            3.1 红黑树的改进

            我们先来看我们写的红黑树的节点代码：

            // 节点结构体
template
struct RBTreeNode
{
	RBTreeNode* _left;
	RBTreeNode* _right;
	RBTreeNode* _parent;
	pair _kv;
	color _col;
	RBTreeNode(pair kv)
		:_left(nullptr),
		_right(nullptr),
		_parent(nullptr),
		_kv(kv),
		_col(Red)
	{}
};

            可以发现，这个节点的设置是写***的，里面的数据就设置为了pair。如果我们想实现set的封装还要在写一份红黑树代码，因为set的节点数据是K 。这样就太不优雅了！

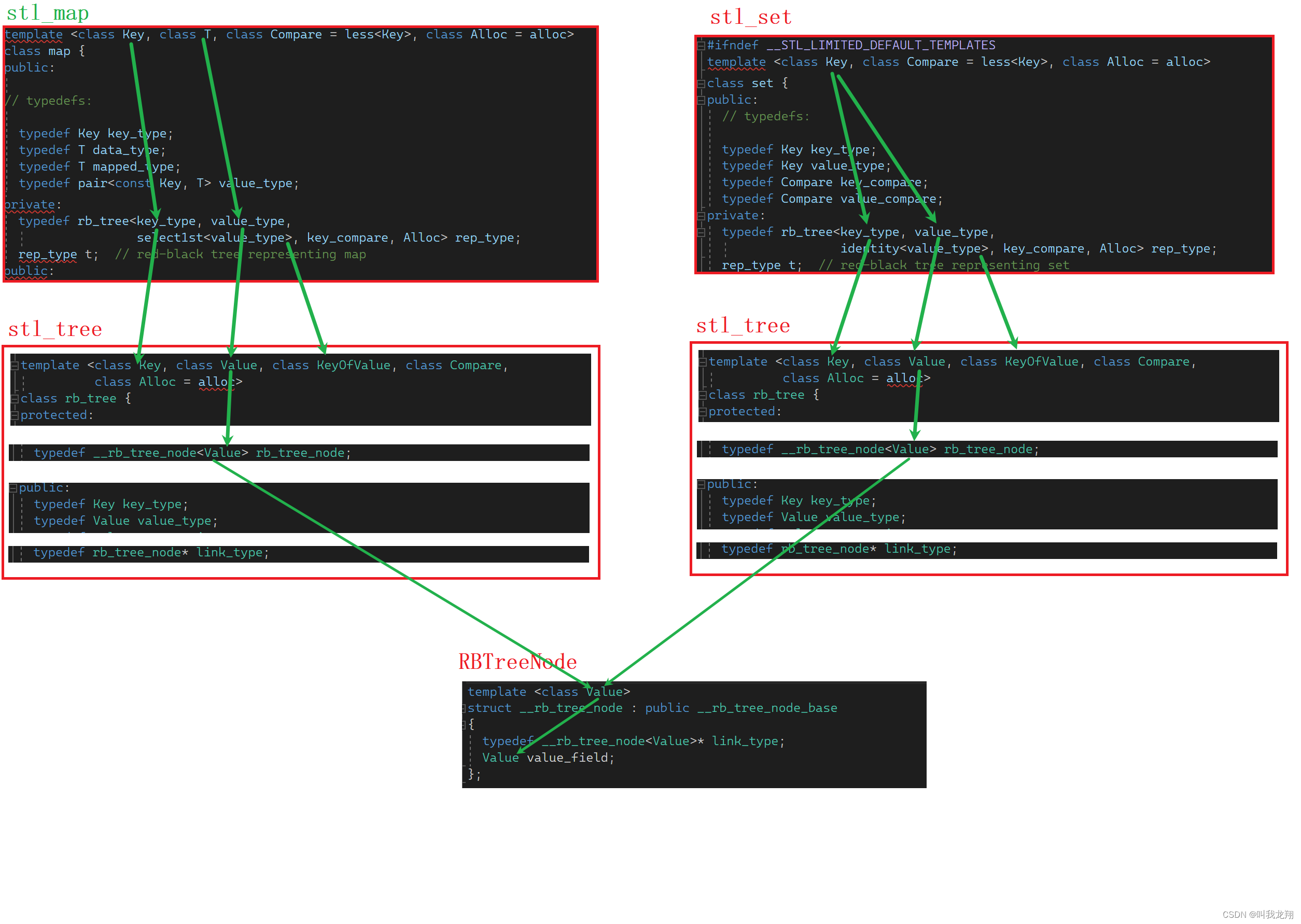
            为了更好实现map与set的封装，我们来看STL源码里是如何实现的吧！

            【C++】从零开始map与set的封装 第2张

            可以看到STL源码中使用了非常巧妙的模版来支持我们上层的map与set:

            1. 首先最底层的节点结构体只使用一个模版参数value，用来表明储存什么数据类型，上层的红黑树通过什么value就使用使用什么
            2. 红黑树这层主要使用Key Value KeyOfValue:
              • KEY：表示键值的类型,在Findj函数里有大用处（利用Key值来寻找是否存在）！！！
              • Value:表示储存的数据类型
              • KeyOfValue：这是一个仿函数，用来从Value取出Key值。
              • map与set这层分别有K V 和 K分别要提供给红黑树Key Value KeyOfValue：
                • map:就传给红黑树
                • set: 就传给红黑树

            这样实现了上层的map与set的模版参数并不一样，却可以使用同一个底层红黑树代码！！！十分巧妙！！！

            我们按照源码改进我们的红黑树：

            //-------------------------------------------
//---------------- 红黑树实现 -----------------
//-------------------------------------------
//-------- 适配map 与 set 的进阶版本 -----------
//-------------------------------------------
#include
enum color
{
	Black,
	Red
};
// 节点结构体
// T在这里是 pair
template
struct RBTreeNode
{	
	RBTreeNode* _left;
	RBTreeNode* _right;
	RBTreeNode* _parent;
	
	T _data;
	color _col;
	RBTreeNode(T data)
		:_left(nullptr),
		_right(nullptr),
		_parent(nullptr),
		_data(data),
		_col(Red)
	{}
};
//适配map与set 的版本
// 迭代器
template
struct _RBTreeIterator
{
	typedef RBTreeNode Node;
	typedef _RBTreeIterator Self;
	Node* _node;
	_RBTreeIterator(Node* node)
		:_node(node)
	{}
	Ref operator*()
	{
		return _node->_data;
	}
	Ptr operator&()
	{
		return &_node->_data;
	}
	bool operator!= (const Self& s)
	{
		return _node != s._node;
	}
	//迭代器的++ 中序遍历的顺序
	Self& operator++()
	{
	}
	Self& operator--()
	{
	}
};
//K 为键值 T 为储存的结构（pair） KeyOfValue 是取出Key的方式
template
class RBTree
{
public:
	typedef _RBTreeIterator Iterator;
	typedef RBTreeNode Node;
	Iterator begin()
	{
		Node* cur = _root;
		while (cur->_left)
		{
			cur = cur->_left;
		}
		return Iterator(cur);
	}
	Iterator end()
	{
		return Iterator(nullptr);
	}
	//右单旋
	void RotateR(Node* parent)
	{
	}
	//左右双旋
	void RotateLR(Node* parent)
	{
	}
	//右左双旋
	void RotateRL(Node* parent)
	{
	}
	//------------------
	//返回需要比较的值
	KeyOfValue kot;
	//------------------
	//插入函数	
	bool Insert(T data)
	{
	}
private:
	void _IsBalance(Node* root , int num)
	{
	}
	bool Check(Node* root, int blackNum, const int refNum)
	{
	}
	void _InOrder(Node* cur)
	{
	}
	RBTreeNode* _root = nullptr;
};

            注意插入函数等里面的比较方式统一改成类似kot(data)

            3.2 map的封装

            实现了红黑树的改进，接下来就简单了！

            在上层操作我们只需要调用对应的底层代码，给予对应的模版参数就好了！！！

            1. map 要满足K V的模版参数的传入
            2. map 要实现一个仿函数用来取出Key
            3. map 类里要有一个底层红黑树类,传入对应的模版参数 (注意键值不可更改哦，所以使用pair)
            4. map 类里要实例化一个迭代器。只需要提供基本的begin()与end()接口（直接调用红黑树的就可以），剩下++ -- ！+交给迭代器操作交给红黑树的迭代器。
            //----------------------------------
//----------  MAP 的实现  -----------
//----------------------------------
#include"RBTree.h"
#include
//层层递进,
//map 上层要提供 key value 键值对
//相应的要改造红黑树的代码 使其满足泛型编程
template
class map 
{
	struct MapOfValue
	{
		const K& operator()(const pair& kv)
		{
			return kv.first;
		}
	};
public:
	typedef typename RBTree::Iterator iterator;
	iterator begin()
	{
		return _t.begin();
	}
	iterator end()
	{
		return _t.end();
	}
	bool Insert(pair kv)
	{
		return _t.Insert(kv);
	}
	void InOrder()
	{
		_t.InOrder();
	}
private:
	//底层是红黑树
	//需要提供对应的键值 储存结构 比较方式
	RBTree _t;
};

            这样就实现了map 的封装！！！

            3.3 set 的封装

            在上层操作我们只需要调用对应的底层代码，给予对应的模版参数就好了！！！

            1. set 要满足K 的模版参数的传入
            2. set 要实现一个仿函数用来取出Key
            3. set 类里要有一个底层红黑树类,传入对应的模版参数 (注意键值不可更改哦，所以使用 const K )
            4. set 类里要实例化一个迭代器。只需要提供基本的begin()与end()接口（直接调用红黑树的就可以），剩下++ -- ！+交给迭代器操作交给红黑树的迭代器。
            //----------------------------------
//----------  SET 的实现  -----------
//----------------------------------
#include"RBTree.h"
#include
//层层递进,
//set 上层要提供 key 键值
//相应的要改造红黑树的代码 使其满足泛型编程
template
class set
{
	struct SetOfValue
	{
		const K& operator()(const K& k)
		{
			return k;
		}
	};
public:
	typedef typename RBTree::Iterator iterator;
	iterator begin()
	{
		return _t.begin();
	}
	iterator end()
	{
		return _t.end();
	}
	bool Insert(K kv)
	{
		return _t.Insert(kv);
	}
	void InOrder()
	{
		_t.InOrder();
	}
private:
	//底层是红黑树
	//需要提供对应的键值 储存结构 比较方式
	RBTree _t;
};

            这样就实现了set的封装！！！

            4 总结

            通过近一周的学习，我们终于将map和set从零建立起来了，这里不仅需要二叉搜索树的知识还需要AVL树和红黑树的使用！！！甚至还需要对于模版的更深理解！！！

            我们写完了发现上层的map和set并没有使用多少代码，大部分是调用底层的代码，所以只有根基稳固才能走到更远！！！

            map和set的封装是很值得回味的内容！！！

            Thanks♪(･ω･)ﾉ谢谢阅读！！！

            下一篇文章见！！！


相关阅读：

1、车VPS定位使用详解，轻松掌握车辆定位技巧，让出行更安心！

2、揭秘，如何完美结合VPS使用BBR技术提速网络？

3、VPS数据库安装与管理全攻略，零基础轻松上手，高效管理技巧揭秘！

4、安卓VPS登陆指南，远程访问与操作一键实现

5、VPS上快速安装ROS，开启机器人操作系统探索之旅！

    高速稳定云服务器25元起
    免责声明：我们致力于保护作者版权，注重分享，被刊用文章因无法核实真实出处，未能及时与作者取得联系，或有版权异议的，请联系管理员，我们会立即处理! 部分文章是来自自研大数据AI进行生成,内容摘自(百度百科,百度知道,头条百科,中国民法典,刑法,牛津词典,新华词典,汉语词典,国家院校,科普平台)等数据,内容仅供学习参考,不准确地方联系删除处理! 图片声明：本站部分配图来自人工智能系统AI生成,觅知网授权图片,PxHere摄影无版权图库和百度，360，搜狗等多加搜索引擎自动关键词搜索配图，如有侵权的图片，请第一时间联系我们，邮箱：ciyunidc@ciyunshuju.com。本站只作为美观性配图使用,无任何非法侵犯第三方意图,一切解释权归图片著作权方,本站不承担任何责任。如有恶意碰瓷者,必当奉陪到底严惩不贷!

    相关阅读

    目录[+]