C语言 图的建立(邻接矩阵与邻接表)
一、邻接矩阵
1.邻接矩阵表示法
邻接矩阵是用于表示图的数据结构之一,可以用二维数组来表示。在邻接矩阵中,每个顶点都对应矩阵的一行和一列,矩阵中的值表示相应两个顶点之间的连通性。如果两个顶点之间存在一条边,则矩阵中对应位置为1;否则为0。如果是网 ,则矩阵中对应位置为权值;否则为(计算机允许、大于所以边上的数)。对于无向图而言,邻接矩阵是对称的;而对于有向图而言,则不一定对称。邻接矩阵可以方便地进行图的遍历、查找和修改等操作,但是对于稀疏图(边数较少)来说,邻接矩阵会浪费大量的空间。
用邻接矩阵表示法表示图除了一个用于储存邻接矩阵的二维数组外,还需要一个一维数组储存顶点信息。
储存结构如下:
#define MVNum 100//最大顶点数
#define MaxInt 66666//表示极大值
typedef struct {
char vexs[MVNum];//顶点表(顶点为字符型)
int arcs[MVNum][MVNum];//邻接矩阵(权值为整型)
int vexnum, arcnum;//图的当前点数和边数
}AMGraph;
2.采用邻接矩阵表示法创建无向网
//定位
int LocateVex(AMGraph* G, char v) {
int i;
for (i = 0; i vexnum; i++) {
if (G->vexs[i] == v) {
return i;
}
}
return -1;
}
//创建无向网G
AMGraph* CreateUDN() {
int i, j, k, w;
char v1, v2;
AMGraph* G = malloc(sizeof(AMGraph));
printf("输入总顶点数,边数\n");
scanf("%d%d", &G->vexnum, &G->arcnum);
getchar();//吸收换行符
printf("依次输入点的信息\n");
for (i = 0; i vexnum; i++) {
scanf("%c", &G->vexs[i]);
}
getchar();//吸收换行符
for (i = 0; i vexnum; i++)
for (j = 0; j vexnum; j++) {
if (i == j) {
G->arcs[i][j] = 0;
}
else {
G->arcs[i][j] = MaxInt;
}
}
for (k = 0; k arcnum; k++) {
printf("输入一条边依附的顶点及权值\n");
scanf("%c%c", &v1, &v2);
scanf("%d", &w);
getchar();//吸收换行符
i = LocateVex(G, v1), j = LocateVex(G, v2);//确定v1、v2在顶点数组的下标
G->arcs[i][j] = w;//边权值置为w
G->arcs[j][i] = w;//无向网对称边权值也置为w
}
return G;
}
再写个输出函数
void print(AMGraph* G) {
int i, j;
printf(" ");
for (i = 0; i vexnum; i++) {
printf("%c ", G->vexs[i]);
}
printf("\n");
for (i = 0; i vexnum; i++) {
printf("%c ", G->vexs[i]);
for (j = 0; j vexnum; j++) {
if (G->arcs[i][j] == MaxInt)
printf("∞ ");
else
printf("%d ", G->arcs[i][j]);
}
printf("\n");
}
}
如果要创建无向图,只需改动两处:一是初始化时将边的权值都初始化为0;二是构造邻接矩阵时将权值w改为1。同样,稍做修改即可建立有向图或有线网(如果你前面知识学懂了,这里肯定没问题)。
二、邻接表
1.邻接表表示法
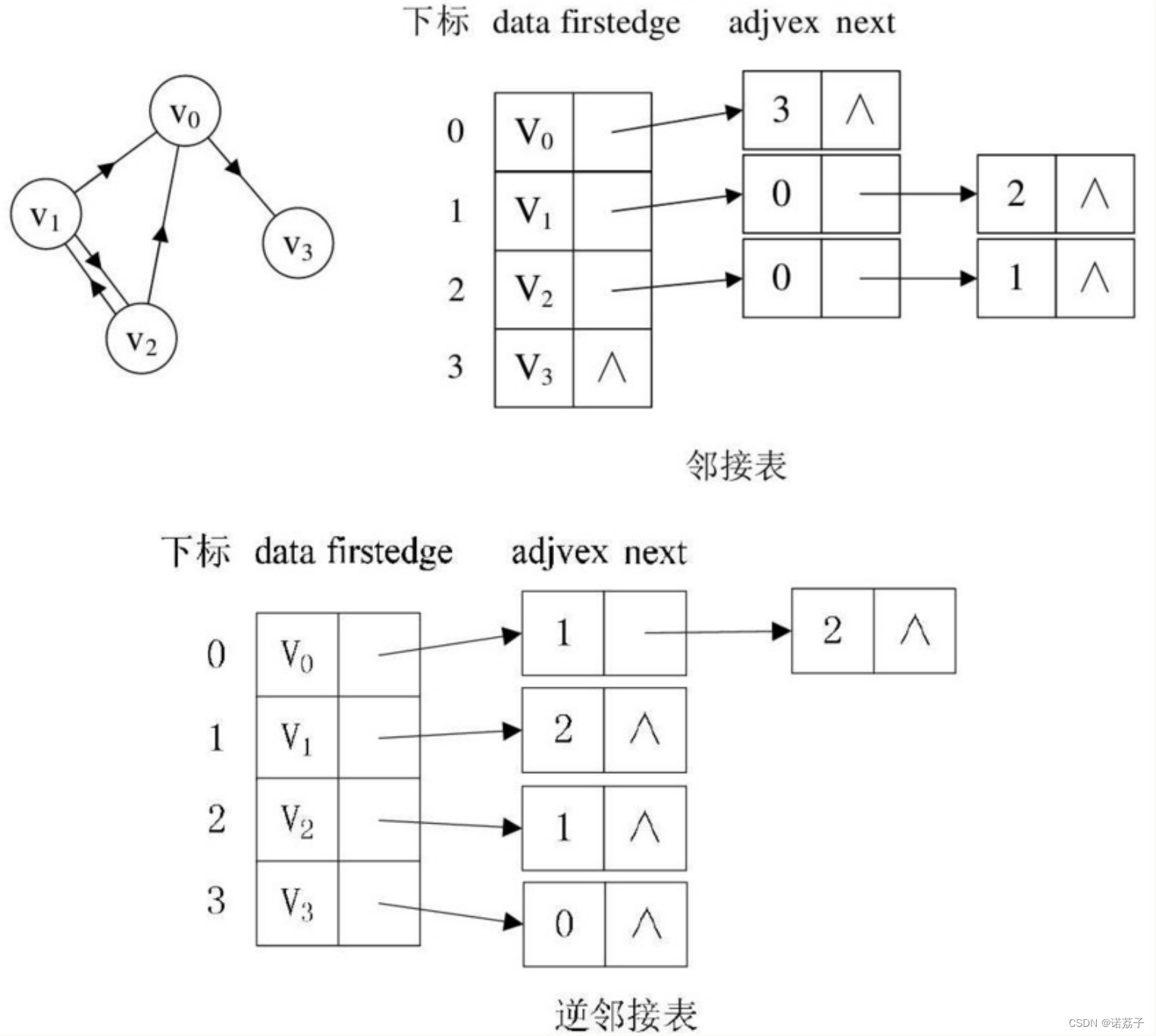
邻接表(Adjacency List)是一种表示无向图或有向图的数据结构。它使用一个数组来存储所有顶点,每个顶点对应一个链表。链表中存储了与该顶点直接相邻的所有顶点。对于有向图,邻接表中的链表只存储指向的顶点(个数为出度)。有时,为了便于确定顶点的入度,可以建立有向图的逆邻接表。
邻接表储存结构如下:
#define MVNum 100 //最大顶点数
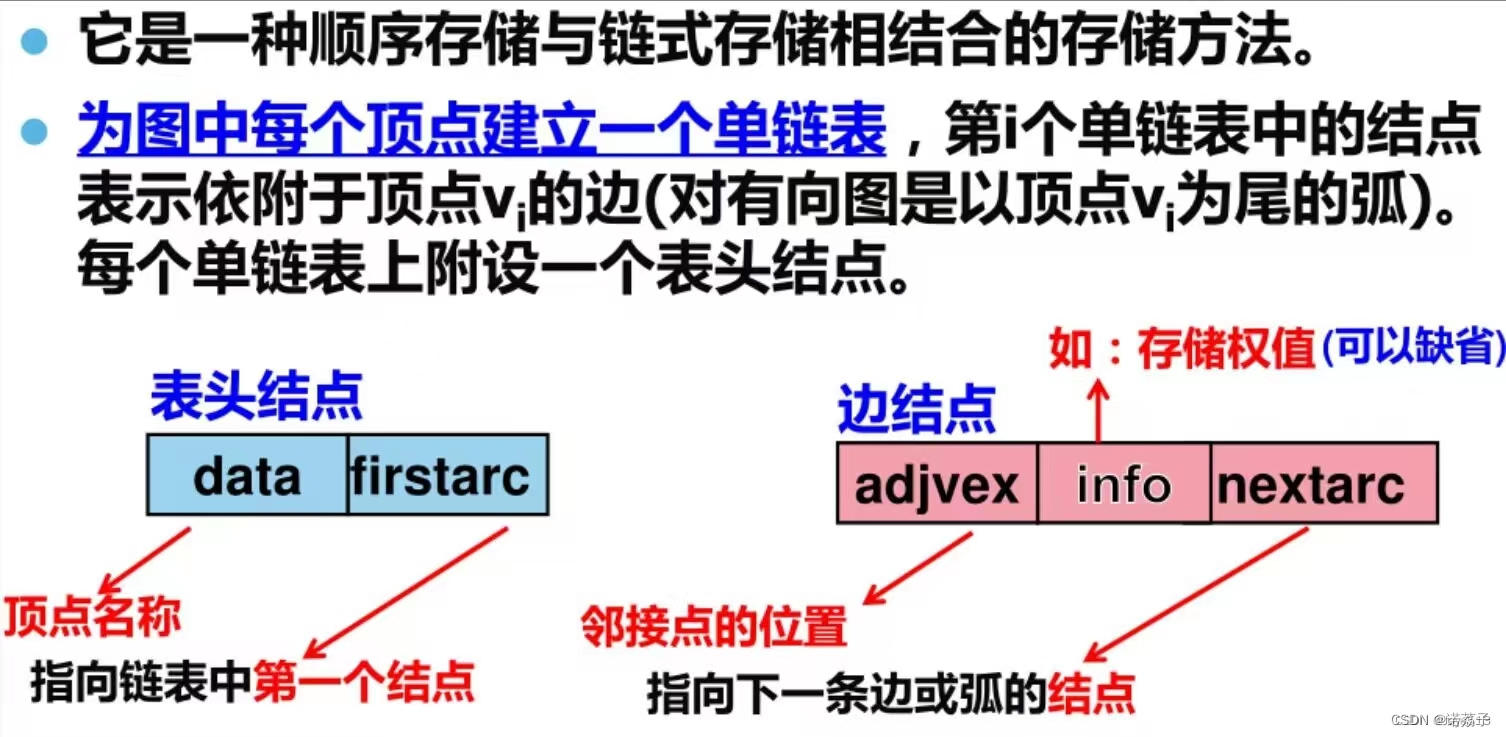
typedef struct ArcNode { //边表结点
int adjvex;//邻接点在顶点数组中的下标
struct ArcNode* next;//指向下一条边的指针
}ArcNode;
typedef struct VNode { //表头顶点信息结构体
char data;
ArcNode* first;//指向第一条依附于该顶点的边的指针
}VNode, AdjList[MVNum];
typedef struct { //图结构体
AdjList vertices;//邻接表
int vexnum, arcnum;//顶点数和边数
}ALGraph;
2.采用邻接表表示法创建无向图
- 首先输入顶点数和边数
- 对于每条边,都会关联两个顶点,所以接下里输入被关联的两个顶点
- 通过输入的顶点调用LocateVex函数来找到这两个顶点在顶点数组中的下标
- 创建新结点,采用头插法插入到关联顶点的表头结点指向的单链表中
//查找 int LocateVex(ALGraph* G, char v) { int i; for (i = 0; i vexnum; i++) { if (G->vertices[i].data == v) { return i; } } return -1; } //无向图的创建 ALGraph* CreateALGraph() { int i, j, k; char v1, v2; ALGraph* G = malloc(sizeof(ALGraph)); printf("输入顶点数和边数:\n"); scanf("%d%d", &G->vexnum, &G->arcnum); getchar();//吸收换行符 printf("依次输入顶点信息:\n"); for (i = 0; i vexnum; i++) { scanf("%c", &G->vertices[i].data); G->vertices[i].first = NULL; } getchar();//吸收换行符 //构造边表 for (k = 0; k arcnum; k++) { printf("输入一条边依附的两个顶点:\n"); scanf("%c%c", &v1, &v2); getchar();//吸收换行符 i = LocateVex(G, v1), j = LocateVex(G, v2);//确定v1、v2在邻接表数组中的下标 ArcNode* p1 = malloc(sizeof(ArcNode));//生成新的边结点*p1 p1->adjvex = i;//邻接点序号为i p1->next = G->vertices[j].first;//头插法插到顶点vj的边表头部 G->vertices[j].first = p1; //因为是无向图,所以生成对称的边结点*p2 ArcNode* p2 = malloc(sizeof(ArcNode)); p2->adjvex = j; p2->next = G->vertices[i].first; G->vertices[i].first = p2; } return G; }还可以写个输出邻接表的函数
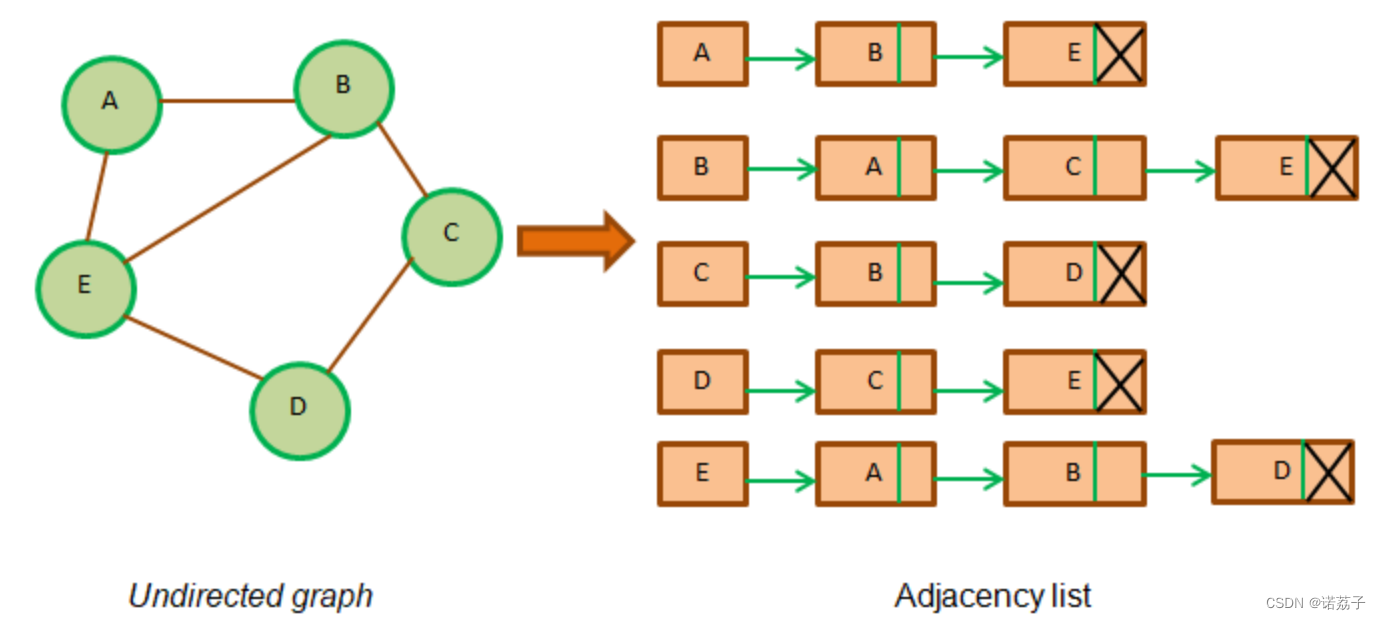
void print(ALGraph* G) { int i; for (i = 0; i vexnum; i++) { printf("顶点%c的邻结点有:", G->vertices[i].data); ArcNode* p = G->vertices[i].first; while (p != NULL) { printf(" %c", G->vertices[p->adjvex].data); p = p->next; } printf("\n"); } }运行 并构建如下图所示的邻接表:
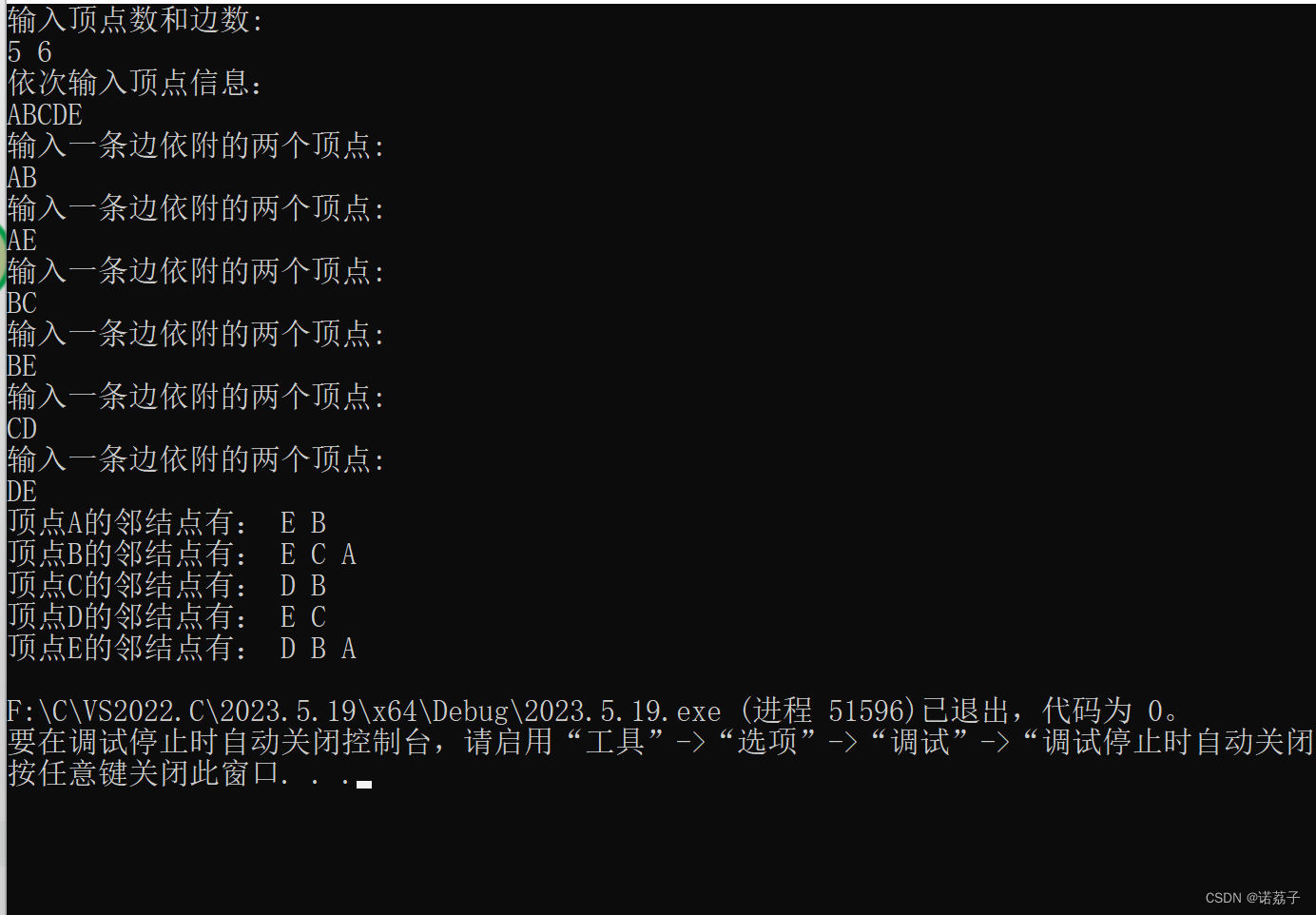
运行结果如下:
总结
免责声明:我们致力于保护作者版权,注重分享,被刊用文章因无法核实真实出处,未能及时与作者取得联系,或有版权异议的,请联系管理员,我们会立即处理!
部分文章是来自自研大数据AI进行生成,内容摘自(百度百科,百度知道,头条百科,中国民法典,刑法,牛津词典,新华词典,汉语词典,国家院校,科普平台)等数据,内容仅供学习参考,不准确地方联系删除处理!
图片声明:本站部分配图来自人工智能系统AI生成,觅知网授权图片,PxHere摄影无版权图库和百度,360,搜狗等多加搜索引擎自动关键词搜索配图,如有侵权的图片,请第一时间联系我们,邮箱:ciyunidc@ciyunshuju.com。本站只作为美观性配图使用,无任何非法侵犯第三方意图,一切解释权归图片著作权方,本站不承担任何责任。如有恶意碰瓷者,必当奉陪到底严惩不贷!