MATLAB : interp1()用法介绍

目录

一、基本语法：

二、实例：

1.样条拟合减振器阻尼曲线

​2.PP拟合时间温度曲线

   interp1 是 MATLAB 中的一个函数，用于在一维数据上执行插值操作。这个函数可以帮助你估计或计算已知数据点之间未知点的值。以下是 interp1 函数的基本用法和参数解释：

一、基本语法：

yi = interp1(x, y, xi, 'method')

• x: 向量，表示已知数据点的 x 坐标或位置。
• y: 向量，与 x 对应的已知数据点的值，即 f(x)。
• xi: 向量或标量，表示你想要进行插值计算的新 x 坐标点位置。
• 'method': 字符串，指定插值方法。MATLAB 支持多种插值方法，包括但不限于：
  • 'linear'（线性插值，默认方法）：通过线性内插估计 y 值。
  • 'nearest'：最近邻插值，选择离 xi 最近的 x 处的 y 值。
  • 'spline'：三次样条插值，提供平滑的曲线拟合。
  • 'cubic'：立方插值，与 'spline' 类似，但在端点处理上略有不同。

  扩展用法:

  • 外插策略:

    yi = interp1(x, y, xi, 'method', 'extrapval')

    其中，'extrapval' 参数指定了在 xi 超出 x 的范围时使用的外推值。 

    • 使用 PP 形式的插值结果:

      pp = interp1(x, y, 'method', 'pp')

       这会返回一个插值对象 pp，之后可以用来计算多个点的插值，提高效率。

              使用 PP 形式的插值结果是指生成一个插值多项式参数向量（Piecewise Polynomial form），在 MATLAB 中通常称为 pp 结构。这种形式的插值结果不是直接给出插值点的值，而是一个可以多次复用的对象，用于高效地计算同一组已知数据点上的多个新点的插值。

      二、实例：

      1.样条拟合减振器阻尼曲线

      %% 进行绘制减振器阻尼特性曲线的样条拟合
      v_d=[-1.04, -0.78, -0.325, -0.13, 0,0.26, 0.52, 0.78, 1.04];
      F_d=[-580, -400, -200, -100, 0,500, 700, 1000, 1400];
      v_vec = -1.04:0.01:1.04;
      F_d_damper = interp1(v_d,F_d,v_vec,'spline');
      figure(1)
      plot(v_vec,F_d_damper);
      xlabel('v_d');
      ylabel('F_d');
      grid on;
      title("F_d的样条曲线","fontsize",16)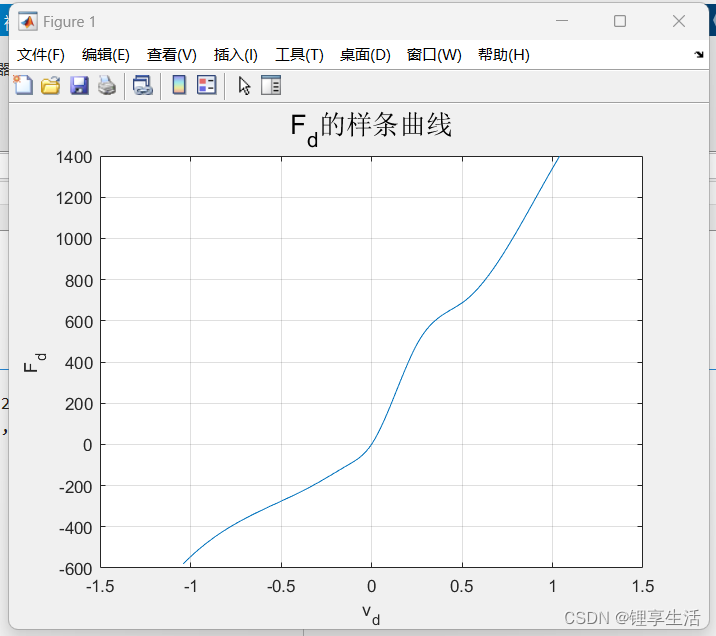
      

       2.PP拟合时间温度曲线

      x = [0, 2, 4, 7, 10]; % 时间点（小时）
      y = [10, 15, 13, 16, 18]; % 对应时间的温度（℃）
      % 创建 PP 结构
      pp = interp1(x, y, 'spline', 'pp');
      xi = [3, 5, 8]; % 我们想要插值的多个点
      yi = ppval(pp, xi);