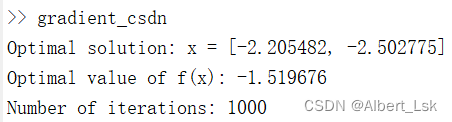【Matlab算法】梯度下降法（Gradient Descent）（附MATLAB完整代码）

梯度下降法优化问题

• 前言
• • 梯度下降法
  • 正文
  • 代码实现
  • • 伪代码
    • 可运行代码
    • 结果

      前言

      梯度下降法

      梯度下降法是一种用于最小化函数的迭代优化算法。其基本思想是通过计算函数的梯度 (导数)，找到函数的最小值点。在梯度下降法中，参数（或变量）沿着负梯度的方向进行更新，以降低函数值。

      以下是梯度下降法的基本描述：

      1. 选择初始点: 选择一个初始点作为优化的起始点。
      2. 计算梯度: 在当前点计算函数的梯度（导数）。梯度是一个向量，包含每个变量的偏导数。
      3. 更新参数：沿着负梯度的方向调整参数。这个调整的步长由一个称为学习率的正数控制，学习率决定了每次更新参数的大小。

         参数 ( t + 1 ) = ^{(t+1)}= (t+1)= 参数 ( t ) − η ⋅ ∇ f ( ^{(t)}-\eta \cdot \nabla f\left(\right. (t)−η⋅∇f( 参数 ( t ) ) \left.^{(t)}\right) (t))

         其中 η \eta η 是学习率， ∇ f ( \nabla f\left(\right. ∇f( 参数 ( t ) ) \left.^{(t)}\right) (t)) 是函数在当前参数点的梯度。

      4. 迭代: 重复步骤2和步骤3，直到满足停止条件，如达到预定的迭代次数或梯度足够小。

      梯度下降法的成功取决于选择合适的学习率、初始点以及停止条件。不同的变种包括随机梯度下降 (SGD) 和批量梯度下降 (BGD)，它们在计算梯度时使用不同的数据集。 SGD使用随机样本，而BGD使用整个数据集。这些变种在不同问题和数据集上表现出不同的性能。

      正文

      对于给出的函数 f ( x ) f(x) f(x) :

      f ( x ) = x ( 1 ) 2 + x ( 2 ) 2 − 2 ⋅ x ( 1 ) ⋅ x ( 2 ) + sin ⁡ ( x ( 1 ) ) + cos ⁡ ( x ( 2 ) ) f(x)=x(1)^2+x(2)^2-2 \cdot x(1) \cdot x(2)+\sin (x(1))+\cos (x(2)) f(x)=x(1)2+x(2)2−2⋅x(1)⋅x(2)+sin(x(1))+cos(x(2))

      计算其梯度，然后使用梯度下降法进行优化。梯度是一个向量，包含每个变量对应的偏导数。对于这个函数，梯度 ∇ f ( x ) \nabla f(x) ∇f(x) 可以通过对每个变量求偏导数得到。

      ∂ f ∂ x ( 1 ) = 2 ⋅ x ( 1 ) − 2 ⋅ x ( 2 ) + cos ⁡ ( x ( 1 ) ) ∂ f ∂ x ( 2 ) = 2 ⋅ x ( 2 ) − 2 ⋅ x ( 1 ) − sin ⁡ ( x ( 2 ) ) \begin{aligned} & \frac{\partial f}{\partial x(1)}=2 \cdot x(1)-2 \cdot x(2)+\cos (x(1)) \\ & \frac{\partial f}{\partial x(2)}=2 \cdot x(2)-2 \cdot x(1)-\sin (x(2)) \end{aligned} ​∂x(1)∂f​=2⋅x(1)−2⋅x(2)+cos(x(1))∂x(2)∂f​=2⋅x(2)−2⋅x(1)−sin(x(2))​

      然后，梯度下降法的更新规则为：

      x ( t + 1 ) = x ( t ) − η ⋅ ∇ f ( x ( t ) ) x(t+1)=x(t)-\eta \cdot \nabla f(x(t)) x(t+1)=x(t)−η⋅∇f(x(t))

      其中 η \eta η 是学习率，是一个控制每次参数更新步长的正数。选择一个合适的学习率，并从初始点 x ( 0 ) x(0) x(0) 开始迭代进行优化。

      这是一个简单的梯度下降法的框架，可以根据具体情况调整参数和终止条件。梯度下降法有不同的变种，例如随机梯度下降 (SGD) 和批量梯度下降 (BGD)，具体的选择取决于问题的性质和数据集的大小。

      代码实现

      伪代码

      % 定义目标函数
      f = @(x) x(1)^2 + x(2)^2 - 2*x(1)*x(2) + sin(x(1)) + cos(x(2));
      % 定义目标函数的梯度
      grad_f = @(x) [2*x(1) - 2*x(2) + cos(x(1)); 2*x(2) - 2*x(1) - sin(x(2))];
      % 设置参数
      学习率 = 0.01;
      最大迭代次数 = 1000;
      容许误差 = 1e-6;
      % 初始化起始点
      x = [0; 0];
      % 梯度下降
      for 迭代次数 = 1:最大迭代次数
          % 计算梯度
          梯度 = grad_f(x);
          
          % 更新参数
          x = x - 学习率 * 梯度;
          
          % 检查收敛性
          if norm(梯度)  
      可运行代码
       
      % 定义目标函数
      f = @(x) x(1)^2 + x(2)^2 - 2*x(1)*x(2) + sin(x(1)) + cos(x(2));
      % 定义目标函数的梯度
      grad_f = @(x) [2*x(1) - 2*x(2) + cos(x(1)); 2*x(2) - 2*x(1) - sin(x(2))];
      % 设置参数
      learning_rate = 0.01;
      max_iterations = 1000;
      tolerance = 1e-6;
      % 初始化起始点
      x = [0; 0];
      % 梯度下降
      for iteration = 1:max_iterations
          % 计算梯度
          gradient = grad_f(x);
          
          % 更新参数
          x = x - learning_rate * gradient;
          
          % 检查收敛性
          if norm(gradient)  
      结果