一级倒立摆控制 —— LQR 控制器设计及 MATLAB 实现
系列文章目录
最优控制介绍
一级倒立摆控制 —— 系统建模(传递函数模型与状态空间方程表示)
一级倒立摆控制 —— PID 控制器设计及 MATLAB 实现
一级倒立摆控制 —— MPC 控制器设计及 MATLAB 实现
文章目录
- 系列文章目录
- 一、一阶倒立摆系统的动力学方程
- 1.1 系统变量表:
- 1.2 一阶倒立摆系统的动力学方程
- 二、LQR控制
- 2.1 确定系统开环极点
- 2.2 设计 LQR 控制器
- 2.2.1 确定系统可控性
- 2.2.2 设计 LQR 控制器
- 2.2.3 改变矩阵 Q Q Q 改进 LQR 控制器
- 2.2.4 增加预补偿环节改进 LQR 控制器
- 2.2.5 基于状态观测器的 LQR 控制器设计
一、一阶倒立摆系统的动力学方程
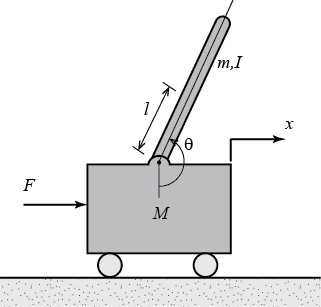
1.1 系统变量表:
参数 符号 数值 小车质量 M M M 0.5 kg 摆杆质量 m m m 0.2 kg 小车摩擦系数 b b b 0.1 N/m/sec 摆杆转动轴心到杆质心的长度 l l l 0.3 m 摆杆转动惯量 I I I 0.006 kg*m^2 施加在小车上的力 F F F 小车位置坐标 x x x 摆杆偏离竖直方向的角度 θ \theta θ 1.2 一阶倒立摆系统的动力学方程
一阶倒立摆系统的动力学方程用状态空间表示为
[ x ˙ x ¨ ϕ ˙ ϕ ¨ ] = [ 0 1 0 0 0 − ( I + m l 2 ) b I ( M + m ) + M m l 2 m 2 g l 2 I ( M + m ) + M m l 2 0 0 0 0 1 0 − m l b I ( M + m ) + M m l 2 m g l ( M + m ) I ( M + m ) + M m l 2 0 ] [ x x ˙ ϕ ϕ ˙ ] + [ 0 I + m l 2 I ( M + m ) + M m l 2 0 m l I ( M + m ) + M m l 2 ] u \begin{bmatrix}\dot{x} \\ \ddot{x} \\ \dot{\phi} \\ \ddot{\phi} \end{bmatrix}= \begin{bmatrix} 0 &1& 0& 0 \\ 0&\dfrac{-(I+ml^2)b}{I(M+m)+Mml^2} &\dfrac{m^2gl^2}{I(M+m)+Mml^2} &0 \\ 0&0&0&1 \\ 0&\dfrac{-mlb}{I(M+m)+Mml^2}&\dfrac{mgl(M+m)}{I(M+m)+Mml^2}&0 \end{bmatrix} \begin{bmatrix}x \\ \dot{x} \\ \phi \\ \dot{\phi} \end{bmatrix}+ \begin{bmatrix}0 \\ \dfrac{I+ml^2}{I(M+m)+Mml^2} \\ 0 \\ \dfrac{ml}{I(M+m)+Mml^2} \end{bmatrix}u x˙x¨ϕ˙ϕ¨ = 00001I(M+m)+Mml2−(I+ml2)b0I(M+m)+Mml2−mlb0I(M+m)+Mml2m2gl20I(M+m)+Mml2mgl(M+m)0010 xx˙ϕϕ˙ + 0I(M+m)+Mml2I+ml20I(M+m)+Mml2ml u
y = [ 1 0 0 0 0 0 1 0 ] [ x ˙ x ¨ ϕ ˙ ϕ ¨ ] + [ 0 0 ] u \bm{y}=\begin{bmatrix}1&0&0&0 \\ 0&0&1&0 \end{bmatrix}\begin{bmatrix}\dot{x} \\ \ddot{x} \\ \dot{\phi} \\ \ddot{\phi} \end{bmatrix}+\begin{bmatrix}0 \\ 0 \end{bmatrix}u y=[10000100] x˙x¨ϕ˙ϕ¨ +[00]u
将上述表格系统值代入得状态空间方程为
[ x ˙ x ¨ ϕ ˙ ϕ ¨ ] = [ 0 1 0 0 0 − 0.1818 2.6727 0 0 0 0 1 0 − 0.4545 31.1818 0 ] [ x x ˙ ϕ ϕ ˙ ] + [ 0 1.8182 0 4.5455 ] u \begin{bmatrix}\dot{x} \\ \ddot{x} \\ \dot{\phi} \\ \ddot{\phi} \end{bmatrix}= \begin{bmatrix} 0 &1& 0& 0 \\ 0&-0.1818 &2.6727 &0 \\ 0&0&0&1 \\ 0&-0.4545&31.1818&0 \end{bmatrix} \begin{bmatrix}x \\ \dot{x} \\ \phi \\ \dot{\phi} \end{bmatrix}+ \begin{bmatrix}0 \\ 1.8182 \\ 0 \\ 4.5455 \end{bmatrix}u x˙x¨ϕ˙ϕ¨ = 00001−0.18180−0.454502.6727031.18180010 xx˙ϕϕ˙ + 01.818204.5455 u
y = [ 1 0 0 0 0 0 1 0 ] [ x x ˙ ϕ ϕ ˙ ] + [ 0 0 ] u \bm{y}=\begin{bmatrix}1&0&0&0 \\ 0&0&1&0 \end{bmatrix}\begin{bmatrix}x \\ \dot{x} \\ \phi \\ \dot{\phi} \end{bmatrix}+\begin{bmatrix}0 \\ 0 \end{bmatrix}u y=[10000100] xx˙ϕϕ˙ +[00]u
二、LQR控制
系统中输出为小车的位置 x x x 和摆杆与竖直方向的角度 ϕ \phi ϕ,小车在 x x x 方向上移动 0.2 m,设计要求如下:
- 位移 x x x 和摆角 ϕ \phi ϕ 的稳定时间小于 5s
- 位移 x x x 的上升时间小于 0.5s
- 摆角 ϕ \phi ϕ 不超过 20°
- 位移 x x x 和摆角 ϕ \phi ϕ 的稳态误差小于 2%
LQR 控制非常适用于多输入多输出变量控制,因此控制要求中保证摆角范围的同时,还要求位移大小。
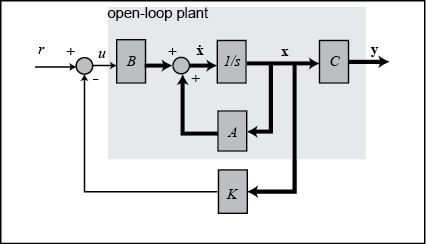
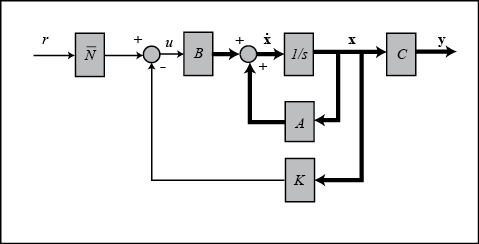
采用全状态反馈控制,控制框图如下
2.1 确定系统开环极点
在一阶倒立摆系统中, r r r 表示小车位置的阶跃指令,4 个状态变量为小车的位置 x x x 和速度 x ˙ \dot{x} x˙,摆杆的角度 ϕ \phi ϕ 和角速度 ϕ ˙ \dot{\phi} ϕ˙,输出为为小车的位置 x x x 和摆杆角度 ϕ \phi ϕ。
参数 符号 位置阶跃指令 r r r 小车位移 x x x 小车速度 x ˙ \dot{x} x˙ 摆杆角度 ϕ \phi ϕ 摆杆角速度 ϕ ˙ \dot{\phi} ϕ˙ 目标为设计一个控制器,当给系统一个阶跃参考值时,摆杆摆动但最终保持竖直状态,小车则移动到指定的位置。
确定系统的开环极点,代码如下
M = 0.5; m = 0.2; b = 0.1; I = 0.006; g = 9.8; l = 0.3; p = I*(M+m)+M*m*l^2; %denominator for the A and B matrices A = [0 1 0 0; 0 -(I+m*l^2)*b/p (m^2*g*l^2)/p 0; 0 0 0 1; 0 -(m*l*b)/p m*g*l*(M+m)/p 0]; B = [ 0; (I+m*l^2)/p; 0; m*l/p]; C = [1 0 0 0; 0 0 1 0]; D = [0; 0]; states = {'x' 'x_dot' 'phi' 'phi_dot'}; inputs = {'u'}; outputs = {'x'; 'phi'}; sys_ss = ss(A,B,C,D,'statename',states,'inputname',inputs,'outputname',outputs); poles = eig(A)输出为
poles = 0 -0.1428 -5.6041 5.5651可以看到,系统只有一个右极点,开环系统是不稳定的。
2.2 设计 LQR 控制器
根据控制框图,需要确定状态反馈矩阵(向量)K,使用状态反馈矩阵的前提是状态变量是可测的。
下面使用 MATLAB 的 lqr() 命令,该命令可以返回最佳状态反馈控制器增益矩阵,该前提是假设系统为线性,代价函数为二次型,
2.2.1 确定系统可控性
在设计 LQR 控制器之前,需要验证系统的可控性。系统可控意味着可以在有限时间内(在系统的物理约束条件下)将系统的状态驱动至任意位置。如果系统是可控的,可控性矩阵的秩为 n。
MATLAB 代码如下
co = ctrb(sys_ss); controllability = rank(co)
输出为
controllability = 42.2.2 设计 LQR 控制器
用线性二次型控制方法来确定状态反馈增益矩阵 K K K, R R R 和 Q Q Q 分别表示在最优化的代价函数中控制输入和误差的相对权重。最简单的情况是令 R = 1 , Q = C ′ C R=1,Q=C'C R=1,Q=C′C,这表示代价函数中对控制输入和对状态变量有相同权重。通过调节控制器中矩阵 Q Q Q 中的非零元素得到合适的响应。
观察矩阵 Q Q Q ,MATLAB 代码如下
Q = C'*C
输出为
Q = 1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0矩阵 Q Q Q 中(1,1)位置的元素表示小车位移的权重,(3,3)位置的元素表示摆杆角度的权重。
权重 R R R 保持为 1,最终起作用的是 Q Q Q 和 R R R 的相对值,而不是绝对值。
根据 Q Q Q 和 R R R 设计 LQR 控制器。MATLAB 代码如下
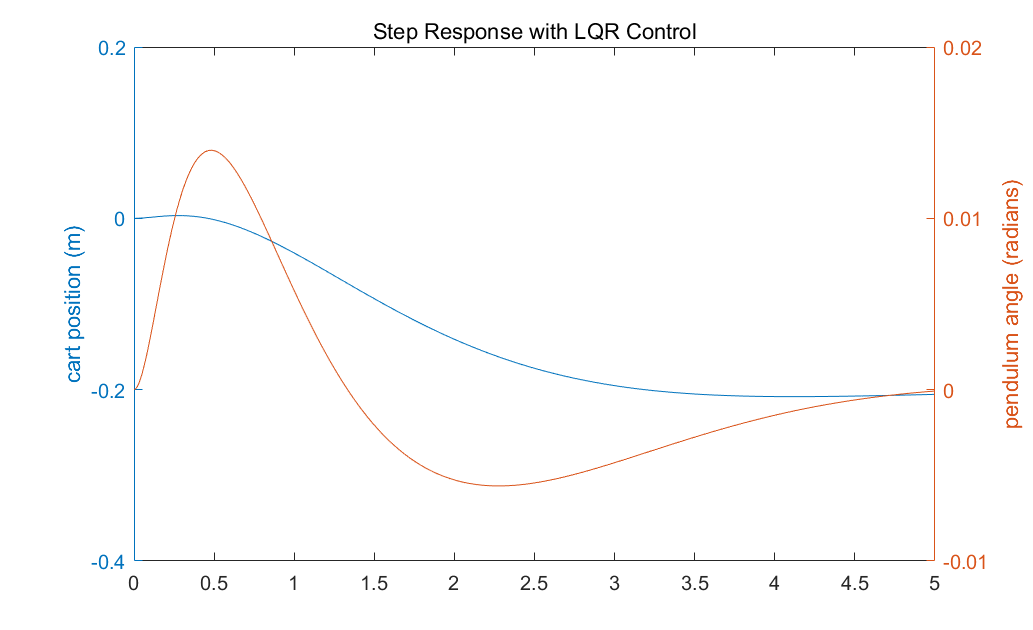
Q = C'*C; R = 1; K = lqr(A,B,Q,R) Ac = [(A-B*K)]; Bc = [B]; Cc = [C]; Dc = [D]; states = {'x' 'x_dot' 'phi' 'phi_dot'}; inputs = {'r'}; outputs = {'x'; 'phi'}; sys_cl = ss(Ac,Bc,Cc,Dc,'statename',states,'inputname',inputs,'outputname',outputs); t = 0:0.01:5; r =0.2*ones(size(t)); [y,t,x]=lsim(sys_cl,r,t); [AX,H1,H2] = plotyy(t,y(:,1),t,y(:,2),'plot'); set(get(AX(1),'Ylabel'),'String','cart position (m)') set(get(AX(2),'Ylabel'),'String','pendulum angle (radians)') title('Step Response with LQR Control')输出为
K = -1.0000 -1.6567 18.6854 3.4594
橙色表示摆杆角度变化曲线,蓝色表示小车位移变化曲线。
回顾控制器的设计要求
- 位移 x x x 和摆角 ϕ \phi ϕ 的稳定时间小于 5s
- 位移 x x x 的上升时间小于 0.5s
- 摆角 ϕ \phi ϕ 不超过 20°
- 位移 x x x 和摆角 ϕ \phi ϕ 的稳态误差小于 2%
摆杆和小车的超调量满足要求,稳定时间需要调整,小车位移 x x x 的上升时间需要减小,小车位移误差需要调整。
2.2.3 改变矩阵 Q Q Q 改进 LQR 控制器
对于小车和摆杆状态变量的稳定时间和上升时间,调整矩阵 Q Q Q 发现,增大矩阵 Q Q Q 中(1,1)和(3,3)位置的元素可以使稳定时间和上升时间下降,减小摆杆移动的角度。这是以增加控制为代价减小误差,即减小稳定时间和上升时间。但是更多的控制意味着需要更大的能量输入。
MATLAB代码如下
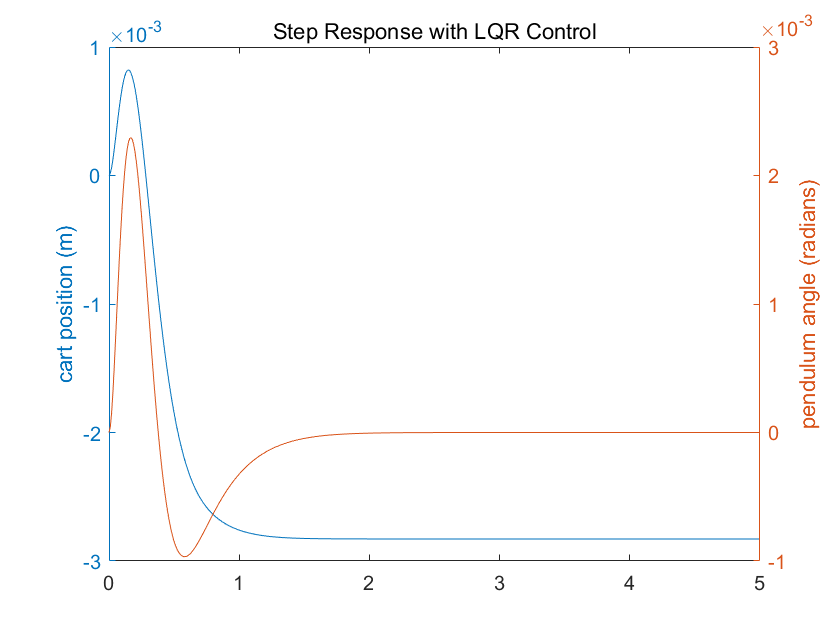
Q = C'*C; Q(1,1) = 5000; Q(3,3) = 100 R = 1; K = lqr(A,B,Q,R) Ac = [(A-B*K)]; Bc = [B]; Cc = [C]; Dc = [D]; states = {'x' 'x_dot' 'phi' 'phi_dot'}; inputs = {'r'}; outputs = {'x'; 'phi'}; sys_cl = ss(Ac,Bc,Cc,Dc,'statename',states,'inputname',inputs,'outputname',outputs); t = 0:0.01:5; r =0.2*ones(size(t)); [y,t,x]=lsim(sys_cl,r,t); [AX,H1,H2] = plotyy(t,y(:,1),t,y(:,2),'plot'); set(get(AX(1),'Ylabel'),'String','cart position (m)') set(get(AX(2),'Ylabel'),'String','pendulum angle (radians)') title('Step Response with LQR Control')输出为
Q = 5000 0 0 0 0 0 0 0 0 0 100 0 0 0 0 0 K = -70.7107 -37.8345 105.5298 20.92382.2.4 增加预补偿环节改进 LQR 控制器
如上框图所示,通过增加预补偿环节 N ‾ \overline{N} N 实现稳态误差最小。预补偿环节 N ‾ \overline{N} N 可以通过函数 rscale.m 实现,rscale.m 文件内容如下
function[Nbar]=rscale(a,b,c,d,k) % Given the single-input linear system: % . % x = Ax + Bu % y = Cx + Du % and the feedback matrix K, % % the function rscale(sys,K) or rscale(A,B,C,D,K) % finds the scale factor N which will % eliminate the steady-state error to a step reference % for a continuous-time, single-input system % with full-state feedback using the schematic below: % % /---------\ % R + u | . | % ---> N --->() ---->| X=Ax+Bu |--> y=Cx ---> y % -| \---------/ % | | % |