吴恩达机器学习-可选实验室-梯度下降-Gradient Descent for Linear Regression

文章目录

• • 目标
  • 工具
  • 问题陈述
  • 计算损失
  • 梯度下降总结
  • 执行梯度下降
  • 梯度下降法
  • 成本与梯度下降的迭代
  • 预测
  • 绘制
  • 祝贺

    

    目标

    在本实验中，你将:使用梯度下降自动化优化w和b的过程

    工具

    在本实验中，我们将使用:

    • NumPy，一个流行的科学计算库
    • Matplotlib，一个用于绘制数据的流行库在本地目录的
    • lab_utils.py文件中绘制例程

      import math, copy
      import numpy as np
      import matplotlib.pyplot as plt
      plt.style.use('./deeplearning.mplstyle')
      from lab_utils_uni import plt_house_x, plt_contour_wgrad, plt_divergence, plt_gradients
      

      当前jupyter note工作目录需要包含：

      

      问题陈述

      让我们使用和之前一样的两个数据点——一个1000平方英尺的房子卖了30万美元，一个2000平方英尺的房子卖了50万美元。

      

      # Load our data set
      x_train = np.array([1.0, 2.0])   #features
      y_train = np.array([300.0, 500.0])   #target value
      

      计算损失

      这是上一个实验室开发的。我们这里还会用到它

      #Function to calculate the cost
      def compute_cost(x, y, w, b):
         
          m = x.shape[0] 
          cost = 0
          
          for i in range(m):
              f_wb = w * x[i] + b
              cost = cost + (f_wb - y[i])**2
          total_cost = 1 / (2 * m) * cost
          return total_cost
      

      梯度下降总结

      线性模型：f（x）=wx+b

      损失函数：J（w，b）

      

      参数更新：

      

      执行梯度下降

      

      

      def compute_gradient(x, y, w, b): 
          """
          Computes the gradient for linear regression 
          Args:
            x (ndarray (m,)): Data, m examples 
            y (ndarray (m,)): target values
            w,b (scalar)    : model parameters  
          Returns
            dj_dw (scalar): The gradient of the cost w.r.t. the parameters w
            dj_db (scalar): The gradient of the cost w.r.t. the parameter b     
           """
          
          # Number of training examples
          m = x.shape[0]    
          dj_dw = 0
          dj_db = 0
          
          for i in range(m):  
              f_wb = w * x[i] + b 
              dj_dw_i = (f_wb - y[i]) * x[i] 
              dj_db_i = f_wb - y[i] 
              dj_db += dj_db_i
              dj_dw += dj_dw_i 
          dj_dw = dj_dw / m 
          dj_db = dj_db / m 
              
          return dj_dw, dj_db
      

      plt_gradients(x_train,y_train, compute_cost, compute_gradient)
      plt.show()
      

      

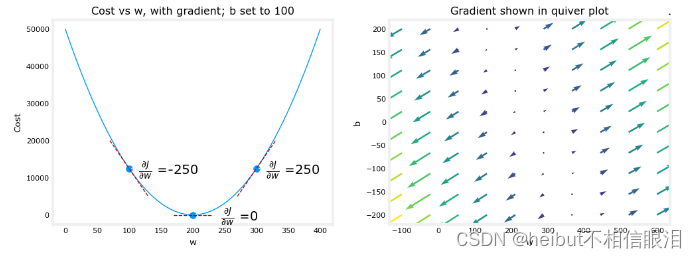
      上面的左边的图固定了b=100。左图显示了成本曲线在三个点上相对于w的斜率。在图的右边，导数是正的，而在左边，导数是负的。由于“碗形”，导数将始终导致梯度下降到梯度为零的底部。

      梯度下降将利用损失函数对w和对b求偏导来更新参数。右侧的“颤抖图”提供了一种查看两个参数梯度的方法。箭头大小反映了该点的梯度大小。箭头的方向和斜率反映了的比例在这一点上。注意，梯度点远离最小值。从w或b的当前值中减去缩放后的梯度。这将使参数朝着降低成本的方向移动。

      梯度下降法

      既然可以计算梯度，那么上面式(3)中描述的梯度下降可以在下面的gradient_descent中实现。在评论中描述了实现的细节。下面，你将利用这个函数在训练数据上找到w和b的最优值。

      def gradient_descent(x, y, w_in, b_in, alpha, num_iters, cost_function, gradient_function): 
          """
          Performs gradient descent to fit w,b. Updates w,b by taking 
          num_iters gradient steps with learning rate alpha
          
          Args:
            x (ndarray (m,))  : Data, m examples 
            y (ndarray (m,))  : target values
            w_in,b_in (scalar): initial values of model parameters  
            alpha (float):     Learning rate
            num_iters (int):   number of iterations to run gradient descent
            cost_function:     function to call to produce cost
            gradient_function: function to call to produce gradient
            
          Returns:
            w (scalar): Updated value of parameter after running gradient descent
            b (scalar): Updated value of parameter after running gradient descent
            J_history (List): History of cost values
            p_history (list): History of parameters [w,b] 
            """
          
          w = copy.deepcopy(w_in) # avoid modifying global w_in
          # An array to store cost J and w's at each iteration primarily for graphing later
          J_history = []
          p_history = []
          b = b_in
          w = w_in
          
          for i in range(num_iters):
              # Calculate the gradient and update the parameters using gradient_function
              dj_dw, dj_db = gradient_function(x, y, w , b)     
              # Update Parameters using equation (3) above
              b = b - alpha * dj_db                            
              w = w - alpha * dj_dw                            
              # Save cost J at each iteration
              if i