【哈希】闭散列的线性探测和开散列的哈希桶解决哈希冲突（C++两种方法模拟实现哈希表）（2）

2024-06-04 7015阅读
【哈希】闭散列的线性探测和开散列的哈希桶解决哈希冲突（C++两种方法模拟实现哈希表）（2） 第1张

🎉博主首页： 有趣的中国人

🎉专栏首页： C++进阶

🎉其它专栏： C++初阶 | Linux | 初阶数据结构

【哈希】闭散列的线性探测和开散列的哈希桶解决哈希冲突（C++两种方法模拟实现哈希表）（2） 第2张

小伙伴们大家好，本片文章将会讲解 哈希函数与哈希 之 哈希桶解决哈希冲突 的相关内容。

如果看到最后您觉得这篇文章写得不错，有所收获，麻烦点赞👍、收藏🌟、留下评论📝。您的支持是我最大的动力，让我们一起努力，共同成长！

🎉系列文章： 1. 闭散列的线性探测实现哈希表

文章目录

  • `0. 前言`
  • `1. 何为开散列`
    • ==🎧1.1 开散列的概念🎧==
    • ==🎧1.2 开散列哈希表图示🎧==
    • `2. 开散列哈希表的实现`
      • ==🎧2.1 开散列哈希表的结构🎧==
      • ==🎧2.2 哈希桶插入Insert🎧==
      • ==🎧2.3 哈希桶查找Find🎧==
      • ==🎧2.4 哈希桶删除Erase🎧==
      • `3. 字符串哈希与仿函数`
      • `4.哈希桶实现哈希表完整代码`

        0. 前言

        在上一篇文章中我们详细描述了如何用 开放寻址法（闭散列）的线性探测 的方法来实现哈希表。此篇文章我们将用 开散列的哈希桶 来实现哈希表。

        1. 何为开散列

        🎧1.1 开散列的概念🎧

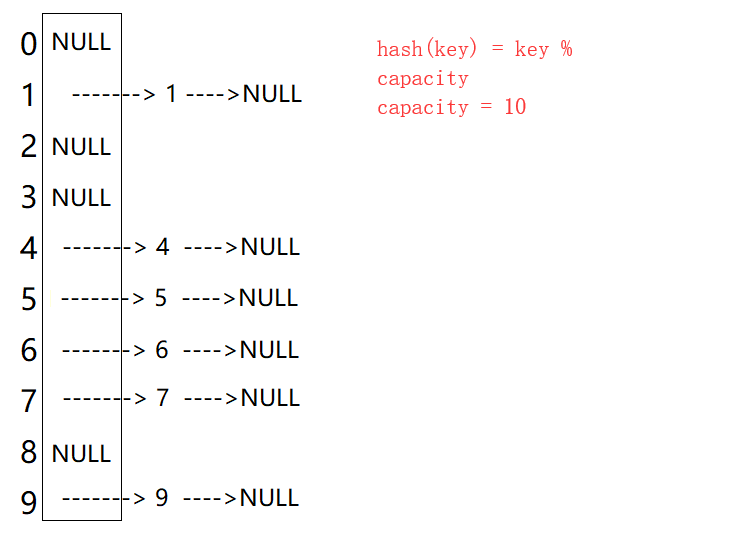
        开散列法又叫链地址法(开链法)，首先对关键码集合用 散列函数计算散列地址，具有相同地址的关键码归于同一子集合，每一个子集合称为一个桶，各个桶中的元素通过一个单链表链接起来，各链表的头结点存储在哈希表中。


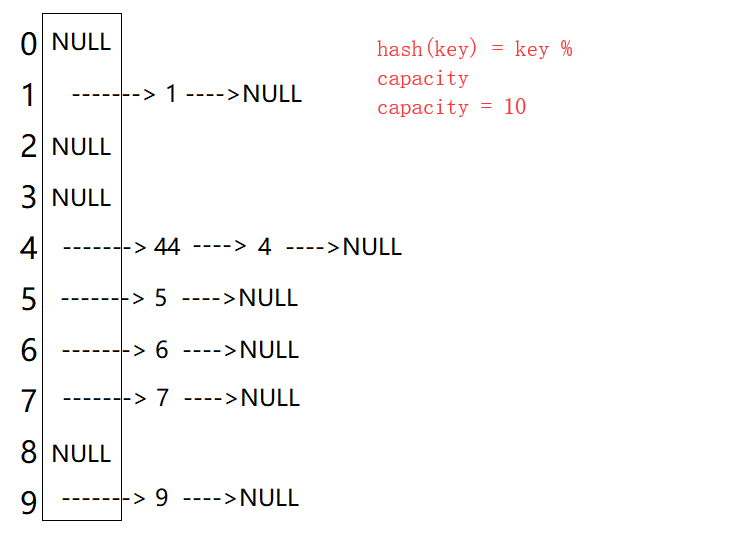
        🎧1.2 开散列哈希表图示🎧

        【哈希】闭散列的线性探测和开散列的哈希桶解决哈希冲突（C++两种方法模拟实现哈希表）（2） 第3张

        插入元素44

        【哈希】闭散列的线性探测和开散列的哈希桶解决哈希冲突（C++两种方法模拟实现哈希表）（2） 第4张

        从上图可以看出，开散列中每个桶中放的都是发生哈希冲突的元素。

        2. 开散列哈希表的实现

        🎧2.1 开散列哈希表的结构🎧

        很明显，这个哈希表中存储了一个指针数组，我们可以用vector来实现，数组中的每个位置存储了一个节点类型的指针，每个节点相当于是链表的一个节点，即：节点中有一个链表类型的指针，还有一个存放值的位置。


        哈希节点和哈希表结构代码：

        // 定义节点类型
template
struct HashNode
{
	// 存储值的位置
	pair _kv;
	// 节点类型指针
	HashNode* _next;
	HashNode(const pair& kv)
		:_kv(kv)
		,_next(nullptr)
	{}
};
// 定义哈希表，第三个模板类型是仿函数，上一篇文章讲过
template
class HashTable
{
public:
	typedef HashNode Node;
	HashTable(size_t n = 10)
	{
		_tables.resize(n);
	}
private:
	// 指针数组
	vector _tables;
	// 存储的元素个数
	size_t _n = 0;
};

        🎧2.2 哈希桶插入Insert🎧

        插入元素的思路：

        1. 利用 哈希函数 计算出 要插入的值应该存放在哪个桶里面；
        2. 之后在对应的桶中进行链表的头插：
          • 首先new一个哈希表的节点newnode；
          • 让 newnode->_next= _tables[i]；
          • 再让newnode当作头：_tables[i] = newnode；
          • ++_n；

        关于哈希桶的扩容：

        在线性探测中，当负载因子 load_factor 在 0.75 0.75 0.75 左右的时候就要进行扩容，但是在哈希桶中，我们可以适当让负载因子大一点，在STL库中，哈希桶的扩容是当负载因子等于 1 1 1 的时候进行扩容，即： n = = t a b l e . s i z e ( ) n == table.size() n==table.size()。

        注意：哈希桶中的负载因子是可以大于1的，因为一个桶中可能存储的不止一个值。

        扩容思路1：

        我们可以继续利用在线性探测的扩容思路：

        1. 新定义一个HashTable的对象newht，表的容量还是两倍；
        2. 遍历原始的HashTable中的vector _tables：
          • 如果_tables[i]不为空，那么就调用newht.Insert()函数；
            • 定义一个节点类型的指针Node* cur = _tables[i]；
            • 调用newht.Insert(cur->_kv);
            • 再让cur = cur->_next；
            • 如果_tables[i]为空，就让i++；
            • 直到 i == _tables.size()，则newht插入完成；
            • 最后两个_tables进行交换：_tables.swap(newht._tables)；

        但是这样扩容虽然可以，但是会很麻烦，因为：

        1. 由于每个哈希节点是new出来的，因此不能直接使用vector的析构函数，要自己写一个析构函数，不然会有内存泄漏；
        2. 每次调用newht.Insert()的时候都会重新new一个节点，原始的节点都会被释放，因此这样操作就会很麻烦编译器。

        扩容代码（version1）：

        // 手动进行析构
~HashTable()
{
	for (size_t i = 0; i _next;
			delete cur;
			cur = next;
		}
	}
}
// 扩容代码
if (_n == _tables.size())
{
	// 方法1：新定义一个对象
	size_t newsize = 2 * _tables.size();
	HashTable newht(newsize);
	for (size_t i = 0; i _next;
			newht.Insert(cur->_kv);
			cur = next;
		}
	}
	_tables.swap(newht._tables);
}

        扩容思路2：

        1. 定义一个新表vector newtables，表的容量还是两倍；
        2. 遍历旧表，如果当前位置不为空，在新表中进行插入，思路如下：
          • 定义一个哈希节点指针Node* cur = _tables[i]；
          • 通过cur->_kv.first 和 哈希函数 计算出 应该插入到新表的哪个桶中(hashi)；
          • 由于插入之后会找不到下一个节点的位置，所以应该再定义一个Node* next = cur->next；
          • 在新表中头插cur，还是同样的思路：
            • 让cur->_next = newtables[hashi]（cur的下一个指向原始的头节点）；
            • 接着让 newtables[hashi] = cur（让cur当头）；
            • 插入完成让cur = next；
            • 直到cur == nullptr，说明此桶中的节点都在新表中插入完成；
            • 让旧表中的_tables[i] = nullptr； （这部也可以不做，因为表不会调用析构函数，但是最好还是置空一下）
            • 如果当前位置为空，则i++；
            • 直到 i == _tables.size()，说明此表的所有元素在新表中插入完成；
            • 最后两表进行交换：_tables.swap(newtables)；

        扩容代码（version2）：

        if (_n == _tables.size())
{
	vector newtable;
	// 两倍的旧表容量
	size_t newsize = 2 * _tables.size();
	newtable.resize(newsize);
	for (size_t i = 0; i _next;
			// 计算在新表中的位置
			size_t hashi = cur->_kv.first % newtable.size();
			// cur的下一个位置指向原来的头
			cur->_next = newtable[hashi];
			// cur当头
			newtable[hashi] = cur;
			// 更新cur的位置
			cur = next;
		}
		// 旧表置空
		_tables[i] = nullptr;
	}
	_tables.swap(newtable);
}

        完整的插入逻辑代码：

        bool Insert(const pair& kv)
{
	// 这边就是上一篇文章的仿函数
	HashFunc hf;
	// 查找思路待会实现
	if (Find(kv.first))
	{
		return false;
	}
	// 判断负载因子扩容
	// 负载因子为1扩容
	if (_n == _tables.size())
	{
		// 方法1：新定义一个对象
		/*size_t newsize = 2 * _tables.size();
		HashTable newht(newsize);
		for (size_t i = 0; i _next;
				newht.Insert(cur->_kv);
				cur = next;
			}
		}
		_tables.swap(newht._tables);*/
		// 方法2：新定义一个表
		vector newtable;
		size_t newsize = 2 * _tables.size();
		newtable.resize(newsize);
		for (size_t i = 0; i _next;
				size_t hashi = hf(cur->_kv.first) % newtable.size();
				cur->_next = newtable[hashi];
				newtable[hashi] = cur;
				cur = next;
			}
			_tables[i] = nullptr;
		}
		_tables.swap(newtable);
	}
	size_t hashi = hf(kv.first) % _tables.size();
	Node* newnode = new Node(kv);
	// 头插
	newnode->_next = _tables[hashi];
	_tables[hashi] = newnode;
	++_n;
	return true;
}

        🎧2.3 哈希桶查找Find🎧

        查找实现思路如下：

        1. 根据 key 和 哈希函数计算出对应的桶(hashi)；
        2. 在此桶中进行寻找：
          • 定义一个哈希节点类型的指针Node* cur = _tables[hashi]；
          • 一直向后寻找，直到找到或者 cur == nullptr（没有此元素）。
          • 找到返回此位置的指针，找不到返回空。

        完整的查找逻辑代码：

        Node* Find(const K& key)
{
	HashFunc hf;
	// 根据 `key` 和 哈希函数计算出对应的桶(`hashi`)
	size_t hashi = hf(key) % _tables.size();
	Node* cur = _tables[hashi];
	while (cur)
	{
		if (cur->_kv.first == key)
		{
			return cur;
		}
		else
		{
			cur = cur->_next;
		}
	}
	return nullptr;
}

        🎧2.4 哈希桶删除Erase🎧

        删除实现思路如下：

        1. 根据 key 和 哈希函数计算出对应的桶(hashi)；
        2. 在此桶中进行查找，这里要考虑要删除的节点的前一个节点是否为空；
        3. 如果前一个节点不为空，直接让prev->_next = cur->_next；
        4. 如果前一个节点为空，就让 _tables[i] = cur->_next；
        5. delete cur; cur = nullptr;
        6. 如果一直到 cur == nullptr 最后都未曾找到，则返回false；
        7. 最后 --_n。

        完整的删除逻辑代码：

        bool Erase(const K& key)
{
	HashFunc hf;
	//  根据 `key` 和 哈希函数计算出对应的桶(`hashi`)；
	size_t hashi = hf(key) % _tables.size();
	Node* cur = _tables[hashi];
	Node* prev = nullptr;
	while (cur)
	{
		if (cur->_kv.first == key)
		{
			// 如果前一个节点为空，就让 `_tables[i] = cur->_next`；
			if (prev == nullptr)
			{
				_tables[hashi] = cur->_next;
			}
			// 如果前一个节点为空，就让 `_tables[i] = cur->_next`
			else
			{
				prev->_next = cur->_next;
			}
			delete cur;
			return true;
		}
		else
		{
			prev = cur;
			cur = cur->_next;
		}
	}
	return false;
}

        3. 字符串哈希与仿函数

        字符串哈希我们上一篇文章讲过：：

        1. 当我们插入数字的类型，例如：double、float、int、 char、unsigned用的是一种类型的哈希函数；
        2. 当我们插入字符串类型string的时候用的是另一种类型的哈希函数；
        3. 🔎遇到这种情况的时候我们一般用仿函数来解决问题！！！🔍

        因此我们要加一个仿函数的模板参数：class HashFunc


        对于数字类型的仿函数代码：

        template
struct Hash
{
	size_t operator()(const K& key)
	{
		// 强转即可
		return (size_t)key;
	}
};

        对于string类型的仿函数代码：

        这里先写一下，待会再细谈：

        struct StringFunc
{
	size_t operator()(const string& str)
	{
		size_t ret = 0;
		for (auto& e : str)
		{
			ret *= 131;
			ret += e;
		}
		return ret;
	}
};

        由于string类型的哈希我们经常用，因此可以用模板的特化，并将此模板用缺省参数的形式传递，这样我们就不用在每次用的时候传入仿函数了。

        template
struct Hash
{
	size_t operator()(const K& key)
	{
		return (size_t)key;
	}
};
template
struct Hash
{
	size_t operator()(const string& str)
	{
		size_t ret = 0;
		for (auto& e : str)
		{
			ret *= 131;
			ret += e;
		}
		return ret;
	}
};

        4.哈希桶实现哈希表完整代码

        🎧有需要的小伙伴自取哈，博主已经检测过了，无bug🎧

        🎨博主gitee链接： Jason-of-carriben 哈希桶实现哈希表完整代码

        【哈希】闭散列的线性探测和开散列的哈希桶解决哈希冲突（C++两种方法模拟实现哈希表）（2） 第5张

        #pragma once
#include 
#include 
using namespace std;
template
struct HashFunc
{
	size_t operator()(const K& key)
	{
		return (size_t)key;
	}
};
template
struct HashFunc
{
	size_t operator()(const string& str)
	{
		size_t hash_value = 0;
		for (auto& e : str)
		{
			hash_value = hash_value * 131 + e;
		}
		return hash_value;
	}
};
namespace hash_bucket
{
	template
	struct HashNode
	{
		pair _kv;
		HashNode* _next;
		HashNode(const pair& kv)
			:_kv(kv)
			,_next(nullptr)
		{}
	};
	template
	class HashTable
	{
	public:
		typedef HashNode Node;
		HashTable(size_t n = 10)
		{
			_tables.resize(n);
		}
		~HashTable()
		{
			for (size_t i = 0; i _next;
					delete cur;
					cur = next;
				}
			}
		}
		bool Insert(const pair& kv)
		{
			HashFunc hf;
			if (Find(kv.first))
			{
				return false;
			}
			// 判断负载因子扩容
			// 负载因子为1扩容
			if (_n == _tables.size())
			{
				// 方法1：新定义一个对象
				/*size_t newsize = 2 * _tables.size();
				HashTable newht(newsize);
				for (size_t i = 0; i _next;
						newht.Insert(cur->_kv);
						cur = next;
					}
				}
				_tables.swap(newht._tables);*/
				// 方法2：新定义一个表
				vector newtable;
				size_t newsize = 2 * _tables.size();
				newtable.resize(newsize);
				for (size_t i = 0; i _next;
						size_t hashi = hf(cur->_kv.first) % newtable.size();
						cur->_next = newtable[hashi];
						newtable[hashi] = cur;
						cur = next;
					}
					_tables[i] = nullptr;
				}
				_tables.swap(newtable);
			}
			size_t hashi = hf(kv.first) % _tables.size();
			Node* newnode = new Node(kv);
			// 头插
			newnode->_next = _tables[hashi];
			_tables[hashi] = newnode;
			++_n;
			return true;
		}
		Node* Find(const K& key)
		{
			HashFunc hf;
			size_t hashi = hf(key) % _tables.size();
			Node* cur = _tables[hashi];
			while (cur)
			{
				if (cur->_kv.first == key)
				{
					return cur;
				}
				else
				{
					cur = cur->_next;
				}
			}
			return nullptr;
			/*for (size_t i = 0; i _next;
					if (cur->_kv.first == key)
					{
						return cur;
					}
					else
					{
						cur = next;
					}
				}
			}
			return nullptr;*/
		}
		bool Erase(const K& key)
		{
			HashFunc hf;
			size_t hashi = hf(key) % _tables.size();
			Node* cur = _tables[hashi];
			Node* prev = nullptr;
			while (cur)
			{
				if (cur->_kv.first == key)
				{
					if (prev == nullptr)
					{
						_tables[hashi] = cur->_next;
					}
					else
					{
						prev->_next = cur->_next;
					}
					delete cur;
					return true;
				}
				else
				{
					prev = cur;
					cur = cur->_next;
				}
			}
			return false;
			//for (size_t i = 0; i _kv.first == key)
			//		{
			//			if (prev == nullptr)
			//			{
			//				_tables[i] = cur->_next;
			//			}
			//			else
			//			{
			//				prev->_next = cur->_next;
			//			}
			//			delete cur;
			//			return true;
			//		}
			//		else
			//		{
			//			prev = cur;
			//			cur = cur->_next;
			//		}
			//	}
			//}
			//return false;
		}
	private:
		vector _tables;
		size_t _n = 0;
	};
	void HashTest1()
	{
		int a[] = { 10001,11,55,24,19,12,31,93,67,26 };
		HashTable ht;
		for (auto e : a)
		{
			ht.Insert(make_pair(e, e));
		}
		ht.Insert(make_pair(32, 32));
		//ht.Insert(make_pair(32, 32));
		ht.Erase(31);
		ht.Erase(10001);
	}
	void HashTest2()
	{
		string arr[] = { "苹果", "西瓜", "苹果", "西瓜", "苹果", "苹果", "西瓜",
	"苹果", "香蕉", "苹果", "香蕉","苹果","草莓", "苹果","草莓" };
		HashTable countMap;
		for (auto& e : arr)
		{
			countMap.Insert(make_pair(e, e));
		}
	}
}

相关阅读：

1、Oracle VPS 6C性能深度解析，核心优势与独特体验揭秘

2、贷款购车可以退款吗？解读贷款购车中的退款问题

3、VPS进入PhpMyAdmin的终极步骤详解

4、欧美VPS与Windows性能大比拼，速度与稳定性的终极对决

5、VPS离线下载Windows，远程文件轻松下载利器

    高速稳定云服务器25元起
    免责声明：我们致力于保护作者版权，注重分享，被刊用文章因无法核实真实出处，未能及时与作者取得联系，或有版权异议的，请联系管理员，我们会立即处理! 部分文章是来自自研大数据AI进行生成,内容摘自(百度百科,百度知道,头条百科,中国民法典,刑法,牛津词典,新华词典,汉语词典,国家院校,科普平台)等数据,内容仅供学习参考,不准确地方联系删除处理! 图片声明：本站部分配图来自人工智能系统AI生成,觅知网授权图片,PxHere摄影无版权图库和百度，360，搜狗等多加搜索引擎自动关键词搜索配图，如有侵权的图片，请第一时间联系我们，邮箱：ciyunidc@ciyunshuju.com。本站只作为美观性配图使用,无任何非法侵犯第三方意图,一切解释权归图片著作权方,本站不承担任何责任。如有恶意碰瓷者,必当奉陪到底严惩不贷!

    相关阅读

    目录[+]