
连续为什么不一定可导?
好的,以下是根据您的要求改写的内容:

标题:《揭秘连续函数不一定可导的原因》
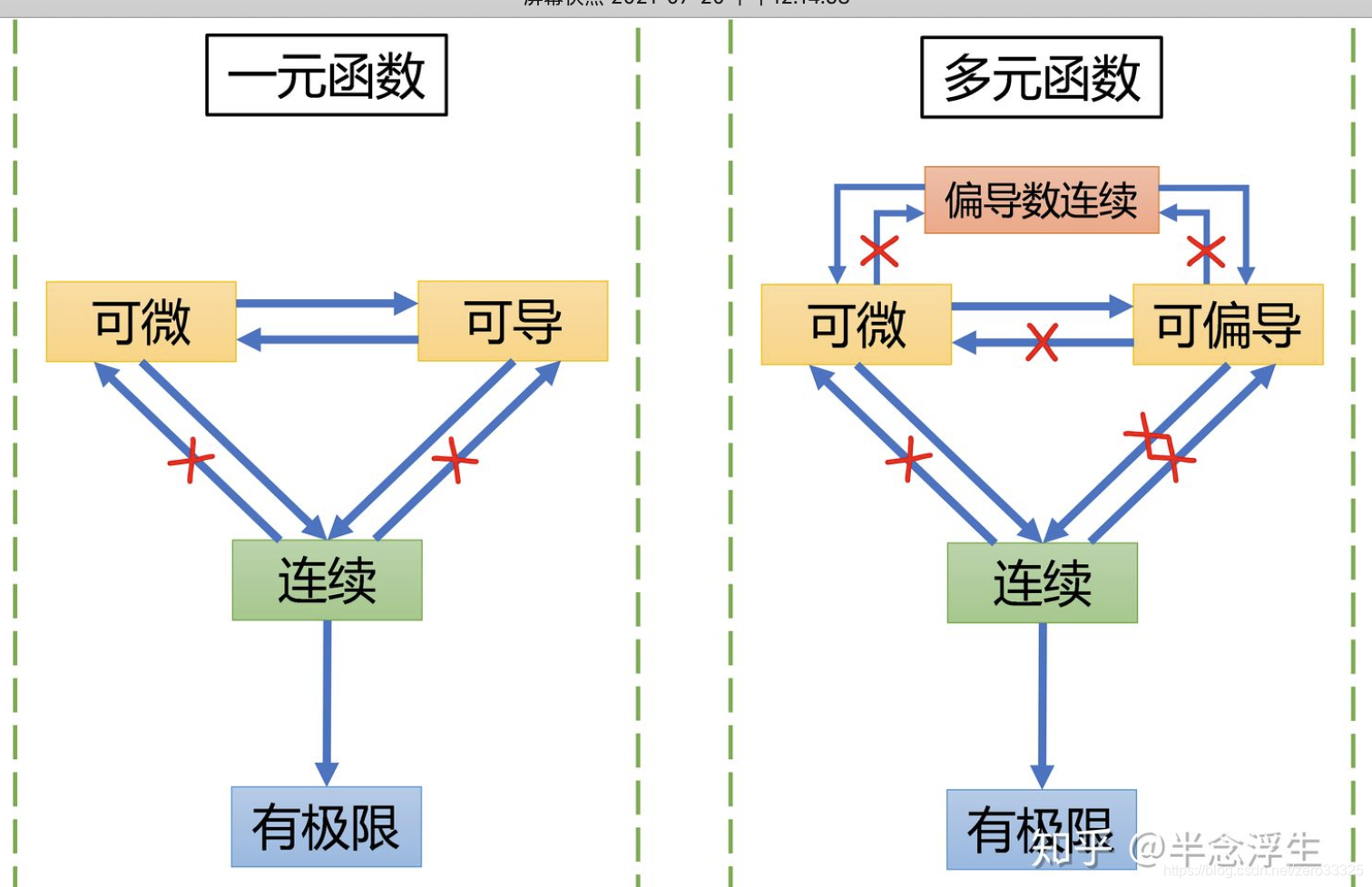
在我们的数学旅程中,我们经常遇到一个充满魅力的概念——“连续”。很多时候,我们容易认为连续就意味着一切都顺理成章,但在数学的世界里,一切都是那么严谨和精确。今天,我们将一起探索一个有趣且重要的现象:为什么连续的函数不一定可导?
首先,我们来理解一下什么是连续和可导。在函数的世界里,连续意味着当我们在函数的定义域内任意取一点,函数值都能平滑过渡到邻近的点。而可导则意味着函数在某一点或某区间内具有确定的斜率,也就是说函数在该点或区间内是平滑变化的。但是,这两者之间并不是必然的联系。也就是说,一个看似平滑的函数可能并不具备在每个点或每个区间内都有明确的斜率。
为什么会这样呢?原因在于函数的性质并不总是完美的。一些函数虽然在定义域内整体上呈现平滑变化的趋势,但在某些特定的点上可能会呈现锐角转折或其他不连续的形态。在这种情况下,函数在这些点上并没有明确的斜率,也就不能称之为可导。这些被称为函数的奇异点或者拐点。即便整个函数看似连续,但在这些点上却失去了可导性。因此,连续性和可导性并不是等价的。尽管两者在大多数情况下是相辅相成的,但在特定的条件下,我们也需要警惕它们之间的差异。
总的来说,连续并不一定意味着可导。在数学的海洋中,每一个概念都有其独特的内涵和边界条件。只有深入理解这些概念的本质和背后的逻辑,我们才能更好地掌握数学的精髓。希望这篇文章能为您揭示连续函数不一定可导的奥秘,激发您对数学世界的探索欲望。





























