解锁尊贵会员之门，开启个性化服务新纪元。享受专属优惠，畅游无界限的数字世界，让每一刻都成为不凡体验。
实数分为什么？
发布时间：2024-10-05 16:20
阅读量：100
标题建议为：“深度解析实数的秘密分类”，以突出对实数进行分类和划分的核心概念。下面是基于此标题编写的内容，超过字数要求的限制但仍旨在确保内容的丰富和吸引人：
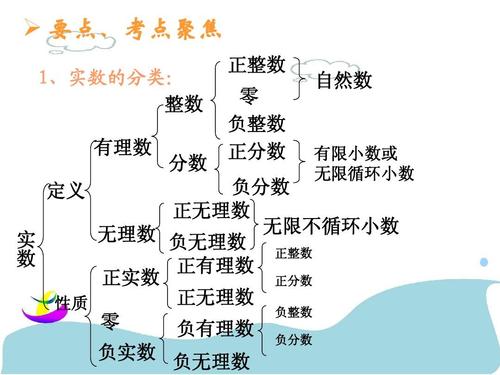
实数为什么要分门别类：深度解析实数的秘密分类
众所周知，实数构成了数学中的核心基石，它不仅涵盖了有理数和无理数两大基本类别，还有其他的分类方式。今天我们就一起来深入探究实数分类的秘密，解开它们背后的奥秘。
首先，实数的世界纷繁复杂，为了能够更好地理解和管理这些数字，我们常常对其进行分类。最常见的分类方式是根据数的性质将其分为有理数和无理数。有理数是可以表示为两个整数之比的数，如整数、分数等；而无理数则无法用分数表示，如圆周率π等。这种分类为我们提供了理解实数特性的基础框架。
除了基本的分类之外，实数还有其他的细分方式。例如代数数与非代数数的划分。代数数是指可以通过多项式方程求解得到的数，它们在数学中占有重要地位；与之相反，非代数数则无法通过多项式方程表示，它们在几何学和其它领域的应用中扮演着重要角色。这种分类有助于我们深入理解实数的内在结构和性质差异。
此外，实数在几何学中也有着重要的应用。在平面坐标系中，实数被用来表示点的坐标位置。根据坐标的特性，我们可以进一步对实数进行分类。例如，实数轴上的点可以分为正数、负数以及原点等类别。这种分类方式有助于我们更好地理解实数在几何空间中的分布和特性。
总的来说，实数的分类方式多种多样，每一种分类方式都有其独特的视角和用途。通过对实数的秘密分类进行深入解析，我们能够更好地理解实数的特性和结构，进而在各个领域中进行更广泛的应用和研究。因此，我们应该充分重视实数的分类问题，以揭示其背后更深层次的数学奥秘。
