解锁尊贵会员之门，开启个性化服务新纪元。享受专属优惠，畅游无界限的数字世界，让每一刻都成为不凡体验。
调和级数为什么发散？
发布时间：2024-10-01 03:40
阅读量：96
好的，以下是根据您的要求生成的文章：
调和级数为什么发散？揭示背后的数学奥秘
你是否曾经遇到过一个数学问题，涉及到调和级数并发现它似乎总是发散，而不是收敛到你预期的结果？今天我们将深入探讨调和级数为什么会发散，揭示其背后的数学原理和逻辑。
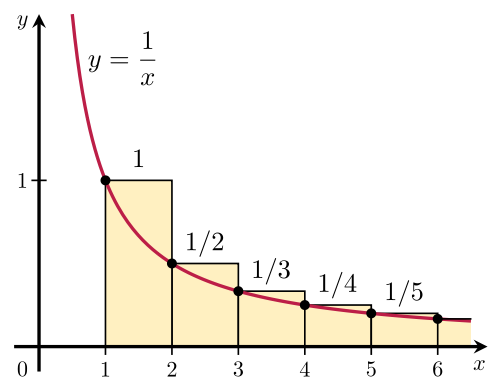
首先，我们需要了解调和级数的定义。调和级数是由一系列递减的分数构成的数列，其分子为常数，分母从1开始逐渐增加。当我们在计算调和级数的部分和时，这些分数的和并不会趋近于某个特定的值，而是无限制地增加。这是因为每个分数的值虽然很小，但由于数列中的项数无限多，这些小的值累积起来会导致部分和不断增大，最终导致发散。
与调和级数形成鲜明对比的是等差数列和等比数列，这两种数列的和在一定条件下可以收敛到有限的值。但调和级数的特性在于其分母的增长速度无法抵消分子累加造成的增长趋势。换句话说，尽管每个分数的值越来越小，但由于分数的数量无限多，它们累积的效果足以让调和级数发散。
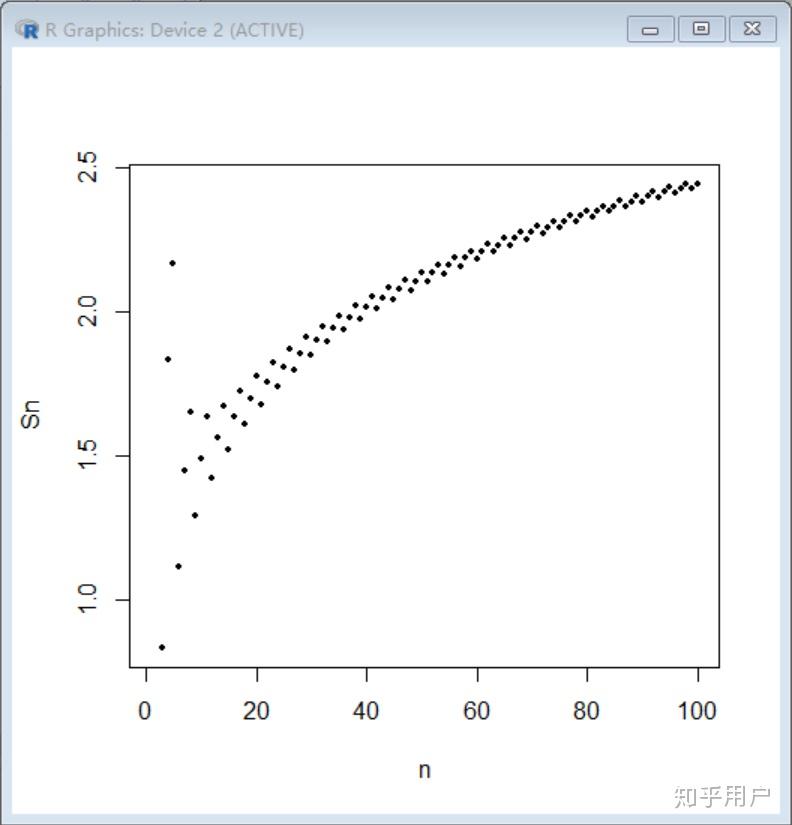
为了更直观地理解这一点，我们可以考虑调和级数的部分和。随着项数的增加，部分和的增长速度会越来越快，因为没有明显的上限来限制它的增长。这种无限制的增长正是调和级数发散的直观表现。
总的来说，调和级数的发散性源于其分子不变而分母逐渐增加的特性，以及无穷多的项数导致的累积效应。这个问题不仅涉及到数学的基本原理，也是无穷级数理论中的重要课题之一。希望这篇文章能帮助你更深入地理解调和级数的奥秘。
